• Introduction
• Calibration
  • Description du fichier d’entrée
  • Étapes de la calibration
    • 1. Empilement des ROIs (patchs)
      • Exemple schématique (notation tensorielle)
    • 2. Alignement spatial (recentrage 3D)
    • 3. Moyennage 3D des volumes alignés
    • 4. Génération des coefficients B-spline 3D
• L’ajustement
  • Description du fichier d’entrée
  • Étapes de l’ajustement
    • 1. Initialisation des éléments
    • 2. Boucle d’ajustement (descente Levenberg-Marquardt)
    • 3. Post-fit : calcul du CRLB (Cramér–Rao Lower Bound)
    • 4. Reconstruction des paramètres globaux
    • 5. Estimation de la confiance (RSS)
• Pour aller plus loin : c’est quoi les coefficients B-Spline

L’analyse de l’ajustement 3D par B-Spline est tiré de SMAP.
COPYRIGHT: Jonas Ries, 2020 LICENSE: GPLv3 AUTHOR: Jonas Ries, EMBL Heidelberg, ries@embl.de

Avant-propos :
Nous allons parler de dimensions et d’indices, de taille…
Voici la nomenclature :
\(x\) : coordonnée x, axe horizontal, colonne de mon tableau.
\(y\) : coordonnée y, axe vertical, ligne de mon tableau.
\(z\) : coordonnée z, axe de plan, profondeur de mon tableau
\(W\) : Largeur totale, nombre de colonnes de mon tableau.
\(H\) : Hauteur totale, nombre de lignes de mon tableau.
\(D\) : Profondeur totale, nombre de plans de mon tableau.

Introduction

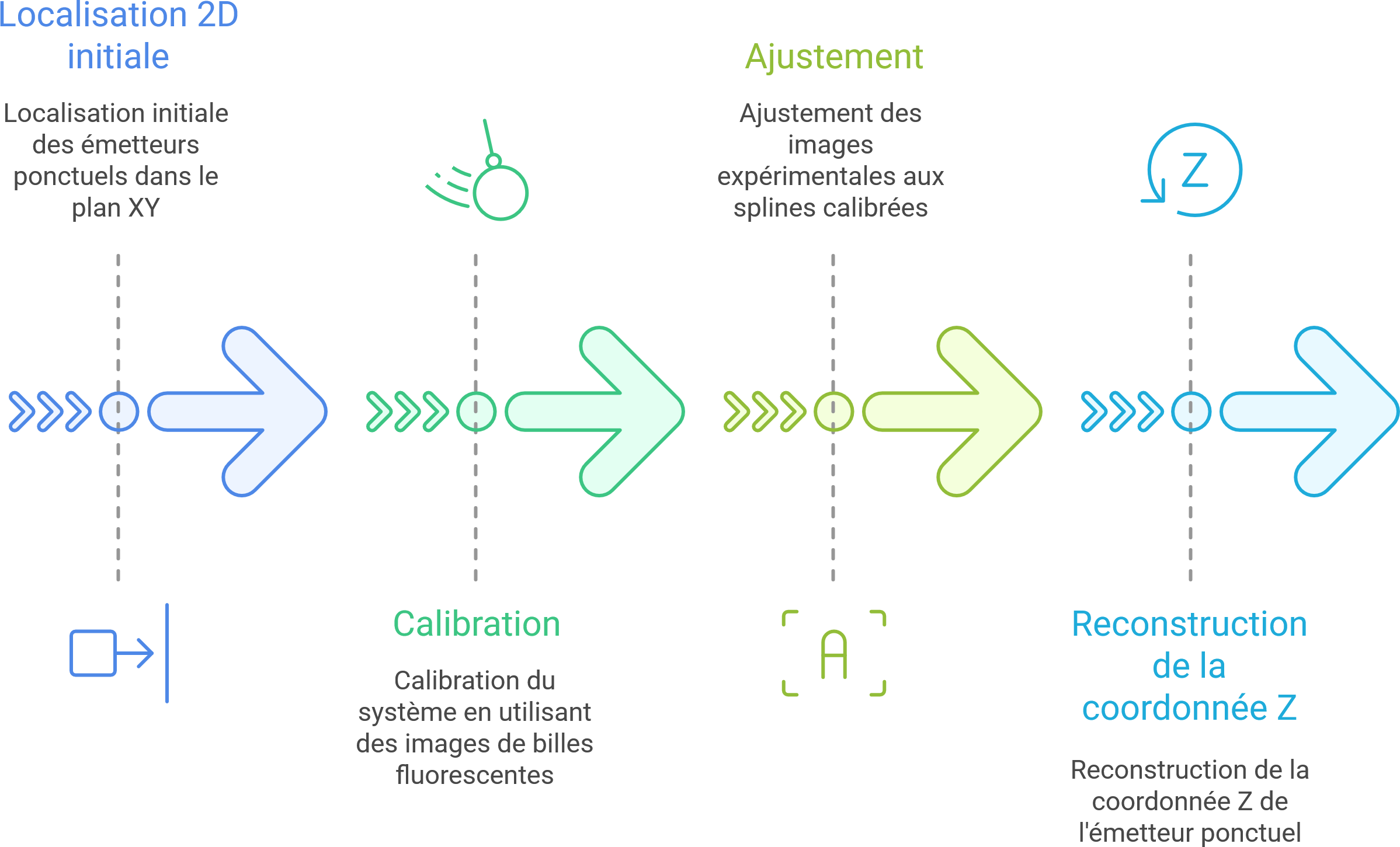
Ce billet présente en détail le processus d’ajustement tridimensionnel par B-splines appliqué à des images issues de microscopie PALM, après localisation 2D initiale.
Le but est de reconstruire la coordonnée \(Z\) d’un émetteur ponctuel à partir de l’ajustement d’un modèle PSF expérimental (et non analytique) représenté par une spline 3D.
Nous supposons que la localisation initiale en \(XY\) est déjà faite (typiquement par du PALM 2D classique), et que ce traitement vise à en déduire une position axiale plus précise, grâce à la forme de la PSF enregistrée.
Deux parties principales participent à ce pipeline :

• La calibration depuis des images de billes fluorescentes.
• L’ajustement des images expérimentales sur ces splines.

Calibration

Description du fichier d’entrée

Le fichier de calibration est une pile 3D d’images de billes fluorescentes capturées à différentes profondeurs focales. Il s’agit d’une pile de N images, chaque plan correspondant à un décalage axial.

• Le nombre de plans Z doit être impair : le plan central correspond à \(Z = 0\).
• L’intervalle entre deux images est constant : \(\Delta z\) (exprimé en nanomètres).
• L’intervalle axial couvert est donc centré sur zéro, allant de :

Chaque bille est localisée en \(XY\), et on extrait un petit cube autour d’elle dans chaque plan \(Z\).

Étapes de la calibration

Le processus repose sur l’analyse de multiples billes pour générer une PSF moyenne bien centrée, représentée sous forme de spline 3D.

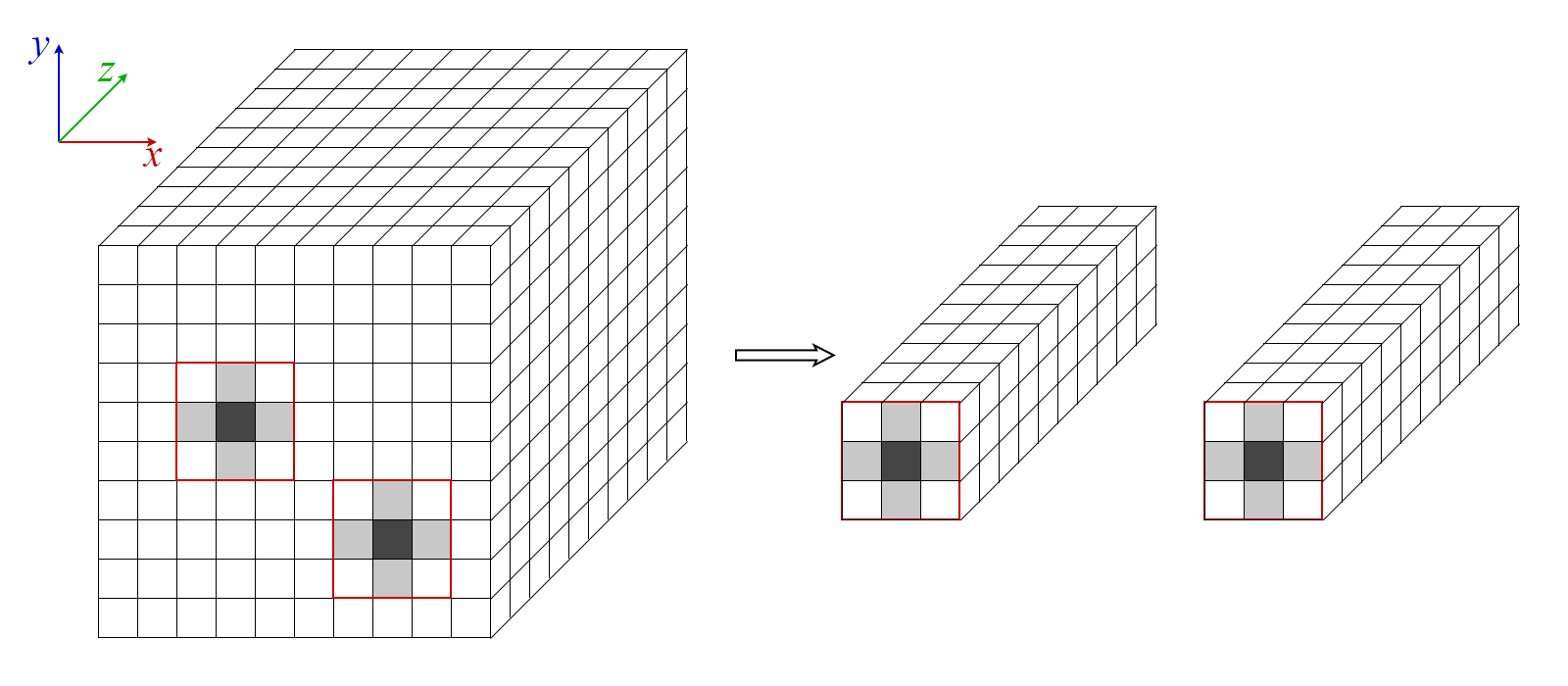
1. Empilement des ROIs (patchs)

On sélectionne pour chaque bille une région d’intérêt 3D (volume) centrée sur sa localisation 2D dans chaque plan de la pile.

• Entrée : Pile d’images de billes (forme : \([x, y, z]\)) + positions XY localisées \((x_i, y_i)\).
• Sortie : Volume 3D par bille \(\rightarrow\) Pile de volumes centrés, forme \([b, [s_{roi}, s_{roi}, z]]\) où \(s_{roi}\) est la taille latérale du patch (en pixels).

Soit \(I[x, y, z]\) l’intensité de la pile en entrée, et une position localisée \((x_i, y_i)\). On extrait pour chaque bille un cube centré sur ces coordonnées :

Où \(s_{roi}\) est la taille latérale du patch (en pixels), \(u,v \in [0, s_{roi}-1]\), et \(z \in [0, D - 1]\).

Exemple schématique (notation tensorielle)

On passe d’une pile d’images : \(I \in \mathbb{R}^{H \times W \times D}\) et d’une liste de \(N_b\) coordonnées 2D : \((x_i, y_i)_{i=1}^{N_b}\) à une pile de ROIs centrés sur chaque bille : \(\texttt{ROIs} \in \mathbb{R}^{N_b \times s \times s\times D }\). Chaque ROI est un petit volume 3D autour d’une bille unique.

2. Alignement spatial (recentrage 3D)

Avant de construire une PSF moyenne représentative, il est crucial d’aligner toutes les régions extraites autour de leur maximum. Chaque volume (ROI) est décalé subpixeliquement pour que le centre d’intensité coïncide avec le centre du volume.
Il faut donc aligner chaque ROI 3D \(\mathrm{ROI}_i[x,y,z]\) autour de son centre optique pour éviter un effet de flou lors de la moyenne.

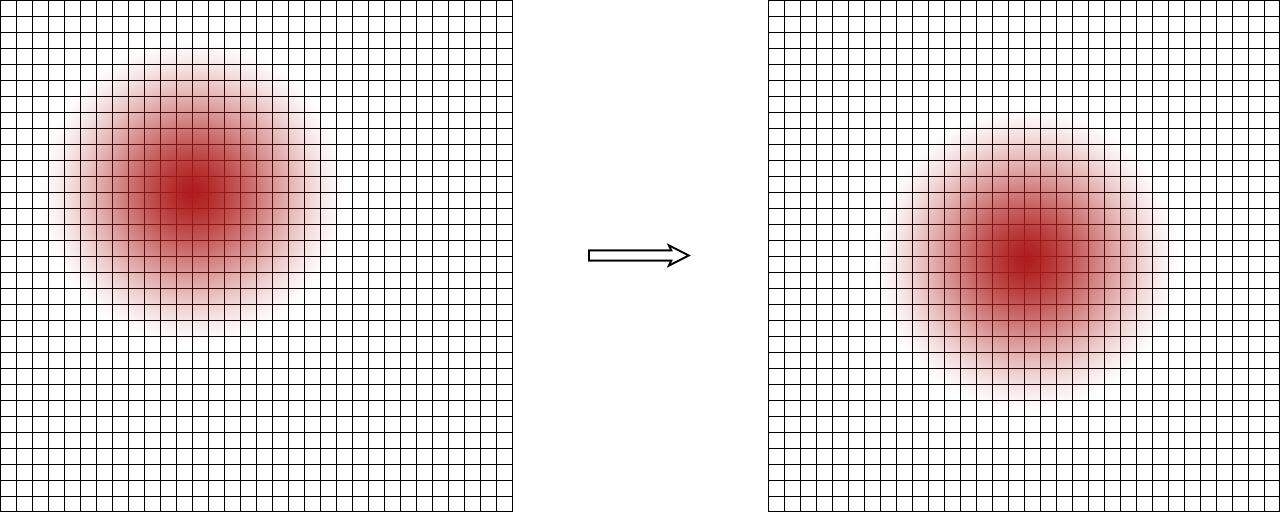
Cela se fait en deux étapes :

1. Estimation du décalage subpixel \((\delta_x, \delta_y, \delta_z)\)
2. Interpolation du volume décalé autour du centre par rééchantillonnage

Pour aligner spatialement chaque volume \(R_i\) autour de son centre, on utilise une méthode robuste de corrélation croisée 3D, combinée à une interpolation subvoxel après suréchantillonnage.
Soit :

• \(R_i\) : la ROI courante
• \(R_{\text{ref}}\) : la référence (moyenne des billes)

Le décalage optimal \((\delta_x, \delta_y, \delta_z)\) correspond au maximum de la fonction de corrélation croisée :

Une interpolation quadratique autour du maximum permet d’atteindre une précision subvoxel.
Pour estimer ce maximum avec une résolution subvoxel, le processus se décompose ainsi :

• Étape 1 – Zoom haute résolution :
  Les deux volumes \(R_i\) et \(R_{\text{ref}}\) sont interpolés avec un facteur de zoom \(F_Z = 2^L\), ici \(L = 2\) soit un facteur de 4. On utilise une interpolation cubique.
• Étape 2 – Normalisation par moyenne :
  Chaque volume haute résolution est normalisé en intensité : \(R' = \frac{R}{\mu_R}, \quad \text{où} \quad \mu_R = \frac{1}{N} \sum\)
  Cette étape est cruciale pour annuler les effets de biais d’intensité entre volumes.
• Étape 3 – Produit de Fourier croisé :
  On applique une FFT 3D sur les deux volumes : \(\widehat{R}_{\text{ref}} = \mathrm{FFT3D}(R_{\text{ref}})\) et \(\widehat{R}_i = \mathrm{FFT3D}(R_i)\)
  Puis on calcule le spectre de phase croisé : \(\widehat{G}(k) = \widehat{R}_{\text{ref}}(k) \cdot \overline{\widehat{R}_i(k)}\)
  Et l’inversion de Fourier donne la fonction de corrélation : \(G(x) = \mathcal{F}^{-1} \left[ \widehat{G}(k) \right]\) Le pic de \(G(x)\) indique le meilleur alignement spatial.
• Étape 4 – Post-traitement de la carte de corrélation :
  • FFT shift : recentrage spatial pour placer le maximum au centre
  • Seuil : on remplace les valeurs négatives par NaN pour exclure les artefacts
  • Normalisation : division par le nombre de voxels valides
• Étape 5 – Recherche du maximum brut :
  On cherche la position \(P\) du maximum de la carte : \(P=\text{Coord}(G_{\max})\)
• Étape 6 – Interpolation subvoxel (subdivision locale) :
  Un raffinement est appliqué autour du maximum à l’aide d’une interpolation locale (souvent quadratique).
  Ce shift est encore dans l’espace suréchantillonné, on le ramène à l’échelle d’origine : \((\delta_x, \delta_y, \delta_z) = \frac{\texttt{shift}}{F_Z}\)

L’algorithme permet un recentrage très précis, typiquement à 1/20 de pixel, ce qui garantit un empilement cohérent des volumes pour le moyennage et l’ajustement par B-spline.
Le volume est ensuite recadré par interpolation cubique. Autrement dit, on applique un décalage de \((\delta_x, \delta_y, \delta_z)\) estimé avec une précision en subvoxel pour recentrer le volume sur son maximum d’intensité.

Cela garantit une parfaite cohérence spatiale pour l’étape de moyennage suivante. On répète encore une fois les différentes étapes d’alignement : Calcul de la moyenne et du décalage à cette nouvelle moyenne suivi de l’application de celui-ci.

3. Moyennage 3D des volumes alignés

Une fois que tous les volumes ont été recentrés au subvoxel autour de leur maximum d’intensité, on peut les fusionner pour construire une PSF moyenne expérimentale, base du modèle spline.

Soit \(R_i^{\text{aligné}}(x,y,z)\) les \(N\) volumes alignés, on définit :

Cette moyenne est voxel par voxel, sur les intensités interpolées.
On peut exclure certaines billes si elles présentent une intensité saturée, un bruit élevé, un fond anormal ou une forme clairement dissymétrique.
Cela se fait généralement via des scores de qualité (corrélation, RMS, etc.), ou un simple filtrage basé sur la valeur maximale / symétrie.

La PSF moyenne obtenue est centrée spatialement (par construction), lissée naturellement par l’effet du moyennage et contient des artefacts minimisés (sauf biais systématique).
Ce volume moyen sera la base pour générer la représentation spline 3D continue de la PSF. Si chaque volume a la forme \([s, s, D]\) (par exemple 9×9×15), la moyenne donne un unique volume : \(\mathrm{PSF}_{\mu} \in \mathbb{R}^{s \times s \times D}\) prêt à être filtré pour obtenir les coefficients spline.

4. Génération des coefficients B-spline 3D

Pour passer d’une PSF discrète (moyenne d’intensité par voxel) à une fonction continue, on représente la PSF moyenne par une combinaison pondérée de B-splines de degré 3 dans chaque dimension.
On cherche à approximer la PSF moyenne comme une somme pondérée de fonctions de base :

où :

• \(c[i,j,k]\) sont les coefficients spline
• \(\beta^3\) est la fonction B-spline de degré 3 centrée

Ce modèle rend possible l’évaluation en n’importe quelle position flottante dans l’espace.

Le filtrage spline consiste à convertir le volume de données \(f[i,j,k]\) (PSF moyenne) en coefficients \(c[i,j,k]\) par un filtrage récursif dans chaque direction.
Le principe est le suivant (1D, généralisé à 3D par axes) :

Pour chaque ligne \(f[n]\), on applique un filtre causal et anticausal basé sur les pôles de la spline cubique :

• Causal (vers l’avant) : \(y_n = f_n + z_1 \cdot y_{n-1}\)
• Anticausal (vers l’arrière) : \(y_n = z_1 \cdot (y_{n+1} - y_n)\)

où \(z_1 = \sqrt{3} - 2\) est le pôle du filtre.

Ce filtrage est appliqué successivement sur X, puis Y, puis Z pour obtenir les coefficients spline 3D avec des conditions aux bords réfléchies (symmetric mirroring), ce qui évite les artefacts et assurant que le gradient d’intensité est nul aux frontières.
Ces coefficients représentent la PSF expérimentale continue, que l’on va désormais utiliser dans la phase d’ajustement.
Les coefficients sont enregistrés sans conversion d’unité : les intensités restent en ADU, les coordonnées sont exprimées en pixels, et aucune mise à l’échelle spatiale n’est appliquée. Le pas axial \(\Delta_z\)​ (en nanomètres) permet uniquement de définir l’échelle d’interpolation sur l’axe Z, entre les différents plans du volume. Il est indispensable pour traduire les positions voxel en profondeur physique lors de l’ajustement.

ℹ️ Remarque importante : les coefficients spline produits par BSpline3D n’encodent pas l’intensité absolue (en ADU), mais uniquement la forme normalisée de la PSF.
En effet, lors de la calibration : les volumes de billes sont centrés, nettoyés et normalisés (soustraction du fond, division par l’énergie maximale), puis moyennés, puis ramenés à une échelle relative.
Ainsi, les coefficients représentent une PSF moyenne unitaire, servant de modèle de forme pour le fit.
L’amplitude réelle d’un point sera retrouvée plus tard comme paramètre indépendant dans la phase d’ajustement.

L’ajustement

L’ajustement des paramètres se fait par minimisation d’une fonction de coûts basée sur le modèle B-spline reconstruit lors de la calibration.

Description du fichier d’entrée

Le fichier d’entrée est une pile 3D d’images (généralement acquise sur le microscope). Il s’agit d’une pile de N images, chaque plan correspondant à une capture dans le temps. La localisation initiale en $XY$ est déjà réalisée par un algorithme de type PALM 2D, ce qui permet de travailler uniquement sur une ROI centrée autour de chaque point.

⚠️ Important : La ROI extraite autour du point localisé ne doit subir aucune normalisation, ni soustraction de fond, ni mise à l’échelle.
Lors de la phase de calibration, la PSF spline a été normalisée pour ne conserver que sa forme (intensité relative).
En théorie, normaliser la ROI ne devrait pas modifier la position \(z\) trouvée, puisque le fit ajuste la forme indépendamment de l’échelle.
Cependant, en pratique, cela fausse les statistiques de bruit utilisées dans la fonction de coût, perturbe l’estimation correcte de l’amplitude et rend le résultat moins cohérent avec d’autres localisations.
Pour cette raison, on recommande de toujours utiliser les ROI brutes, non modifiées.

Étapes de l’ajustement

1. Initialisation des éléments

Pour chaque point localisé :

• On extrait une ROI centrée sur \((x_i, y_i)\) dans la pile 3D.

• On calcule le centre de masse de cette ROI pour initialiser \(x\) et \(y\) de façon robuste :

  \[(x_c, y_c) = \frac{1}{\sum I} \sum I(x, y) \cdot (x, y)\]
• On initialise les paramètres du fit \(\vec{p} = \left[\text{offset}, \text{amplitude}, x, y, z\right]\) avec des bornes minimales et maximales.
• Un paramètre de saut (jump) est défini pour chaque composante, limitant l’évolution d’un pas à l’autre.

2. Boucle d’ajustement (descente Levenberg-Marquardt)

Chaque itération consiste à :

1. Calculer les décalages relatifs \(\delta_x, \delta_y, \delta_z\) entre la ROI et le modèle spline, en tenant compte d’un offset d’alignement (cas où la ROI est plus petite que le modèle spline).
2. Interpoler le noyau spline 3D centré à la position \((x,y,z)\) courante. Cela donne :
   • \(f\) : le noyau spline
   • \(\partial f / \partial x, y, z\) : dérivées partielles

3. Calculer la fonction de coût (log-vraisemblance EMCCD) sur l’ensemble des pixels :

   \[\mathcal{L} = \sum_{i} \left[ 2 (m_i - d_i) - 2 d_i \log\left( \frac{m_i}{d_i} \right) \right]\]

   avec \(m_i\) la valeur modélisée, et \(d_i\) la donnée. Cette formulation est adaptée aux caméras EMCCD, combinant bruit de lecture et statistique de comptage (Poisson).

4. Calcul du Jacobien \(J\) et de l’Hessienne \(H\).
   Le Jacobien correspond au gradient de la fonction de coût, et l’Hessienne à sa courbure. Ces deux objets permettent de choisir la direction et l’échelle du pas optimal dans l’espace des paramètres.

   \[J_i = \frac{\partial \mathcal{L}}{\partial \theta_i}, \quad H_{ij} = \frac{\partial^2 \mathcal{L}}{\partial \theta_i \partial \theta_j}\]

5. Régularisation Levenberg-Marquardt.
   Le terme \(\lambda\) sert à interpoler entre descente de gradient (si \(\lambda\) est grand) et descente de Newton (si \(\lambda\) est petit). Cela stabilise l’optimisation lorsque l’hessienne est mal conditionnée.

   \[H \leftarrow H + \lambda I\]

6. Factorisation de Cholesky de \(H\).
   On tente de factoriser \(H\) sous la forme \(H = LU\) avec \(L\) triangulaire inférieure et \(U\) supérieure (Cholesky). Cela permet de résoudre efficacement le système linéaire pour mettre à jour les paramètres.

   • Si la factorisation réussit : on poursuit avec la descente par LU (substitutions forward/backward)
   • Sinon : la hessienne est instable, on augmente \(\lambda\) pour renforcer la régularisation

7. Mise à jour du vecteur de paramètres $\vec{p}$ avec contrôle de bornes et saut maximum.

8. Critères d’arrêt :

   • Nombre d’itérations maximal
   • Convergence : variation relative faible

3. Post-fit : calcul du CRLB (Cramér–Rao Lower Bound)

Une fois l’ajustement convergé, on calcule la borne de Cramér-Rao (CRLB) pour chaque paramètre.
C’est l’écart-type théorique minimal sur chaque paramètre, obtenu à partir de la matrice d’information de Fisher \(F\) :

4. Reconstruction des paramètres globaux

Les paramètres \((x, y, z)\) sont retransformés dans le repère absolu de l’image :

5. Estimation de la confiance (RSS)

On calcule deux valeurs :

• \(\text{RSS}_{XY} = \frac{1}{2}(\text{CRLB}_x + \text{CRLB}_y)\) (en pixels) : erreur quadratique moyenne sur la localisation latérale.
• \(\text{RSS}_Z = \text{CRLB}_z\) (en voxels). Elle peut être convertie en nanomètres par \(\text{RSS}_{Z_{nm}} = \Delta_z \cdot \text{CRLB}_z\) si besoin.

Ces valeurs donnent une idée de la précision attendue sur chaque paramètre, exprimée dans leur unité naturelle (pixels ou voxels), ou convertie en unités physiques si l’on dispose de l’échelle correspondante.

Chaque point ainsi traité produit une localisation enrichie : \([x, y, z, \text{Intensité}, \text{Offset}, \text{RSS}_{XY}, \text{RSS}_Z]\).

ℹ️ Remarque : Cette méthode suppose que la PSF expérimentale est stable dans le temps et que les conditions d’acquisition sont constantes. Des dérives instrumentales ou des variations de PSF peuvent compromettre la qualité de l’ajustement.

Pour aller plus loin : c’est quoi les coefficients B-Spline

Prenons un petit vecteur de pixels 1D \(\left[0, 1, 3, 7, 9, 7, 3, 1, 0\right]\) : C’est une forme de cloche centrée.
Ici, les valeurs représentent l’intensité au centre de chaque pixel.
En d’autres termes :

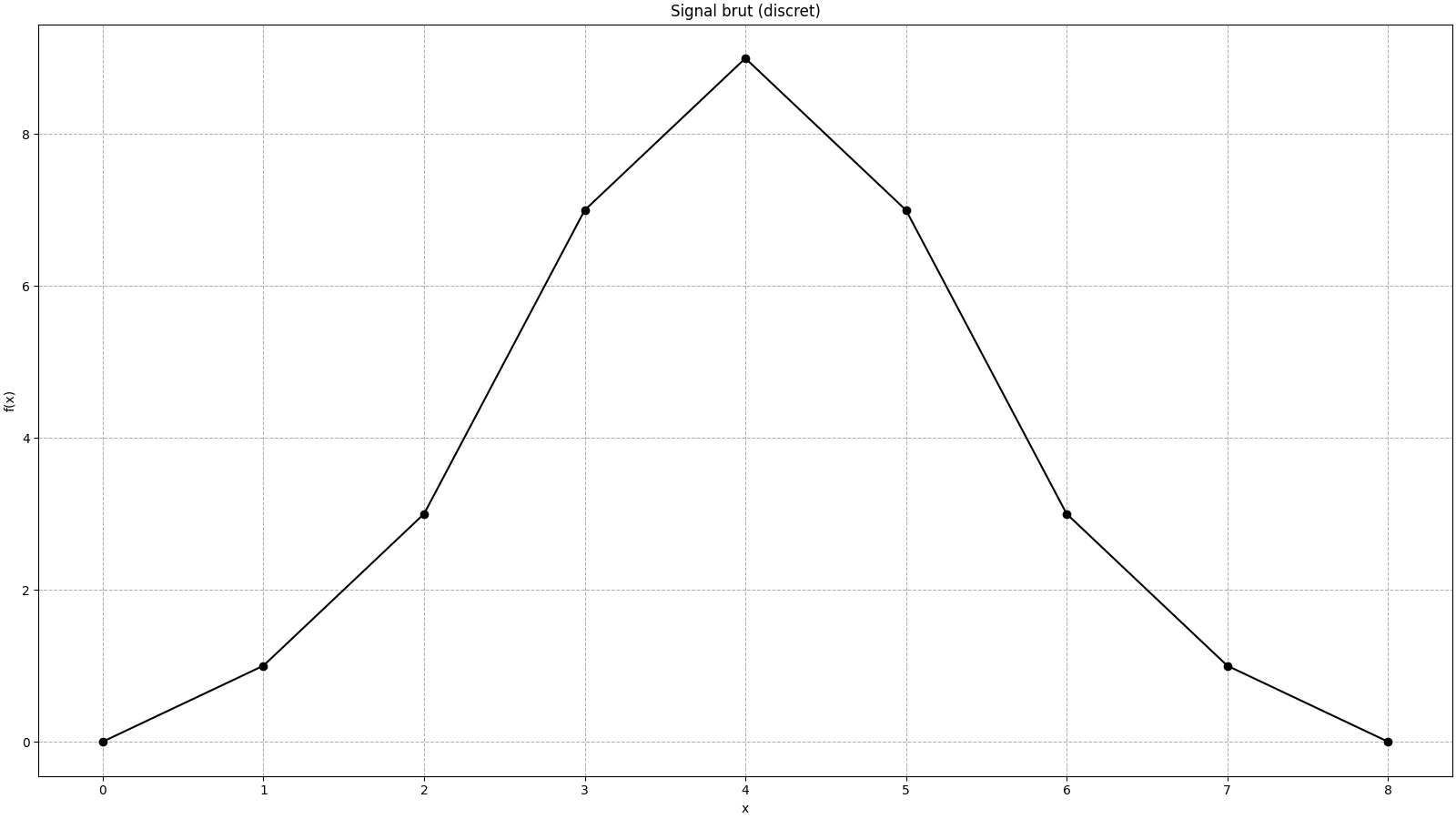
Lors de la transformation du signal en spline cubique, il est représenté comme une somme pondérée de fonctions B-spline centrées sur chaque point entier :

Les \(c_i\)​ sont les coefficients spline, calculés par filtrage.

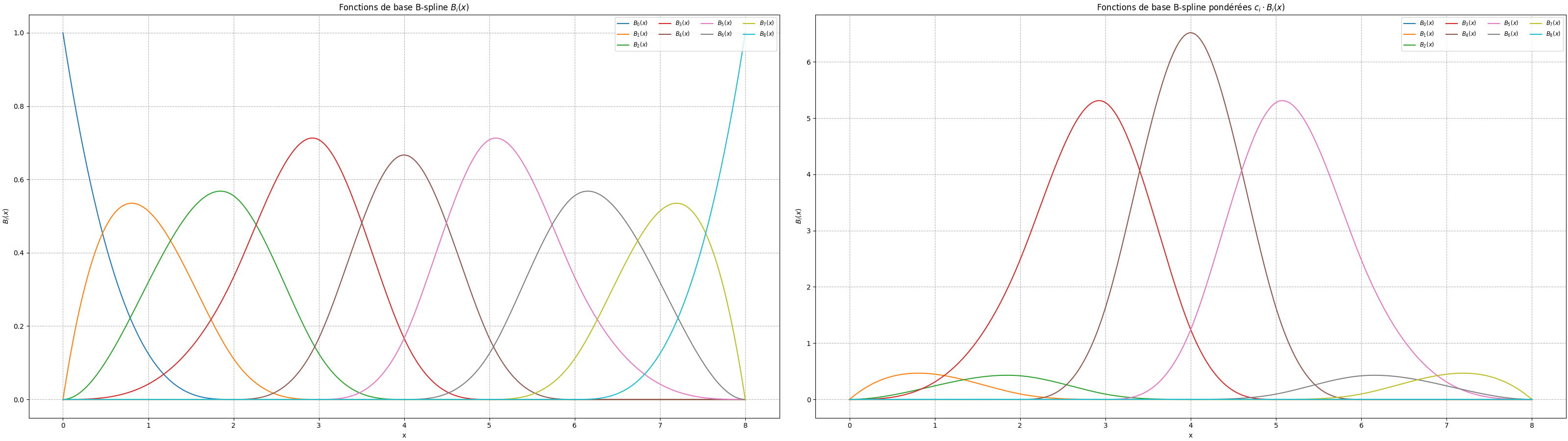
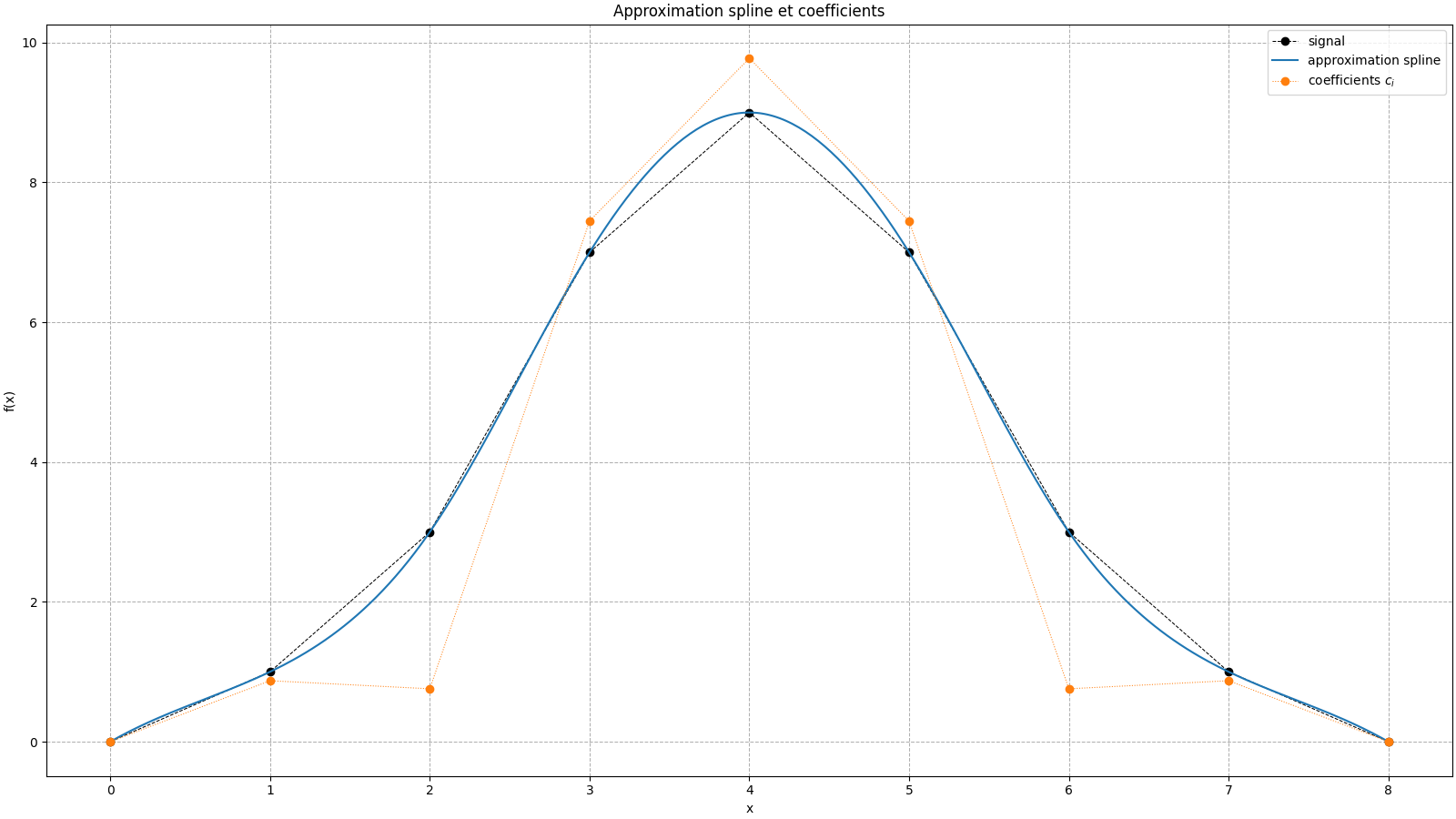
On observe que les coefficients \(c_i\) ne ressemblent pas au signal, mais leur combinaison reproduit précisément sa forme.

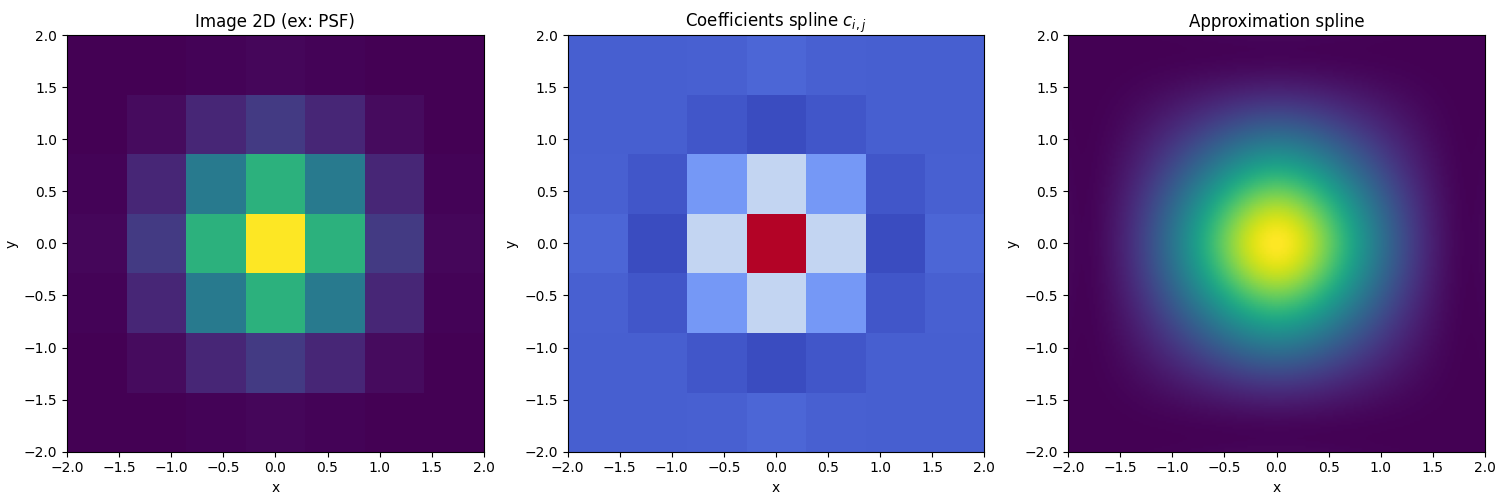
En ajoutant une dimension, nous pouvons simuler la version 2D.

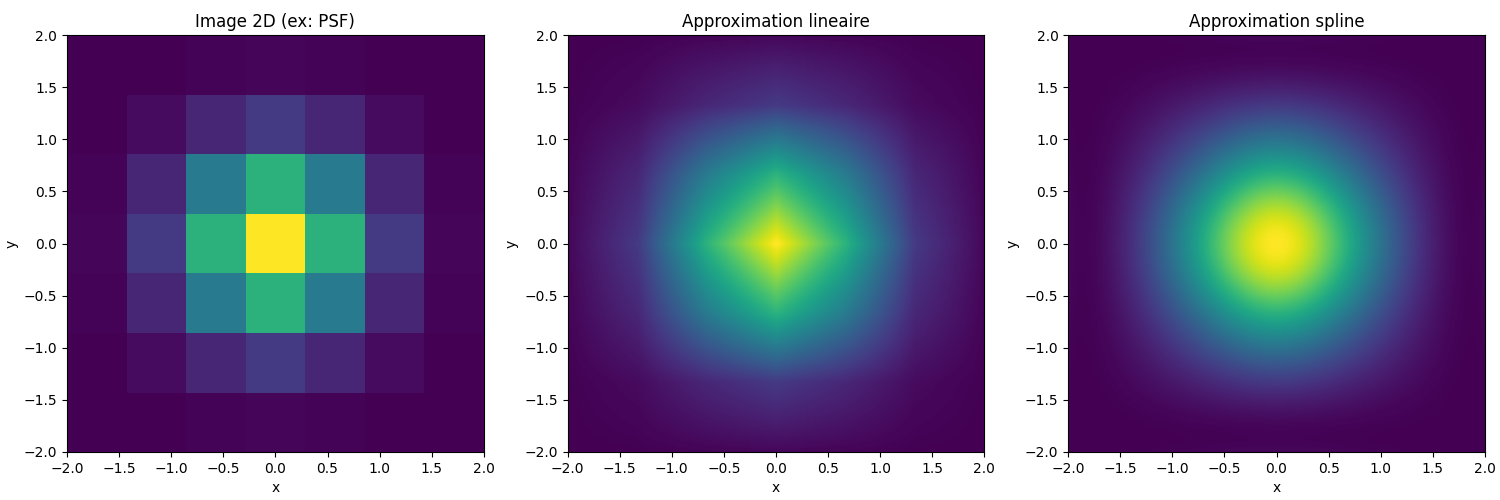
L’utilisation de l’interpolation par B-Spline est complexe, mais plus fiable qu’une simple interpolation linéaire.

Pour la 3D, il suffit de rajouter encore une dimension de coefficients :

Thibaut Monseigne

Ingénieur Recherche et Développement en Interface Cerveau-Machine.