Les risques dans la classification

Déséquilibre des classes
Normalisation des données

Déséquilibre des classes

Un déséquilibre entre deux classes dans un jeu de données peut présenter plusieurs risques :

Biais de classification : Lorsque les classes sont déséquilibrées, le modèle peut être enclin à attribuer une plus grande importance à la classe majoritaire, car il cherche à minimiser l’erreur globale. Cela peut entraîner un biais de classification, où le modèle a du mal à bien identifier les échantillons de la classe minoritaire.
Performances déséquilibrées : Lorsque les classes sont déséquilibrées, les performances du modèle peuvent être biaisées en faveur de la classe majoritaire. Par exemple, si la classe majoritaire représente 90% des échantillons et la classe minoritaire seulement 10%, un modèle naïf qui prédit toujours la classe majoritaire atteindrait déjà une précision de 90% sans apprendre les motifs de la classe minoritaire.
Erreurs coûteuses : Dans certains cas, les erreurs de classification sur la classe minoritaire peuvent être plus coûteuses que les erreurs sur la classe majoritaire. Par exemple, dans un système de détection de fraudes, une fausse alarme sur une transaction légitime est généralement moins grave que de manquer une transaction frauduleuse. Si la classe minoritaire représente les transactions frauduleuses, un déséquilibre peut entraîner des conséquences coûteuses.
Manque de généralisation : Un déséquilibre entre les classes peut rendre difficile la généralisation du modèle à de nouvelles données ou à des scénarios différents. Le modèle peut être suroptimisé pour la classe majoritaire et avoir du mal à bien généraliser les motifs de la classe minoritaire.

Pour atténuer ces risques, il est souvent recommandé de prendre des mesures pour équilibrer les classes, telles que l’over-sampling de la classe minoritaire, l’under-sampling de la classe majoritaire ou l’utilisation de techniques d’ensemble qui combinent les deux approches. Ces méthodes visent à fournir un jeu de données plus équilibré, permettant au modèle d’apprendre de manière plus équitable et de mieux représenter les deux classes.

Sur-Échantillonnage (Over-sampling)

L’over-sampling, qui consiste à augmenter artificiellement le nombre d’échantillons de la classe minoritaire, peut être bénéfique pour résoudre le déséquilibre de classes dans un problème de classification.

Cependant, il y a aussi des risques associés à l’over-sampling, notamment :

Surapprentissage : L’over-sampling peut conduire à un surapprentissage si les échantillons synthétiques générés sont trop similaires aux échantillons d’origine. Cela peut entraîner une surconfiance du modèle dans ses prédictions, ce qui le rend moins généralisable aux nouvelles données.
Amplification du bruit : En créant des échantillons synthétiques, il existe un risque d’amplification du bruit. Si les échantillons de la classe minoritaire sont bruités ou mal étiquetés, l’over-sampling peut étendre ces erreurs et affecter négativement les performances du modèle.
Redondance d’informations : L’over-sampling peut introduire une redondance d’informations dans le jeu de données, car les échantillons synthétiques peuvent être similaires aux échantillons existants. Cela peut entraîner une augmentation de la complexité et de la taille du modèle sans améliorer réellement sa performance.
Biais dans les estimations : L’over-sampling peut introduire un biais dans les estimations de performance du modèle. Comme les échantillons synthétiques sont générés à partir de la classe minoritaire, le modèle peut sembler performant lors de l’évaluation, mais pourrait ne pas généraliser correctement aux données réelles.

Il est important de prendre en compte ces risques potentiels lors de l’utilisation de l’over-sampling. Il est recommandé d’évaluer attentivement les performances du modèle sur des données non vues auparavant et d’utiliser des méthodes supplémentaires, telles que la validation croisée, pour obtenir une évaluation plus robuste du modèle.

Sous-Échantillonnage (Under-Sampling)

L’under-sampling consiste à réduire le nombre d’échantillons de la classe majoritaire afin de les équilibrer avec la classe minoritaire. Cela peut aider à prévenir le surapprentissage et à améliorer les performances du modèle.

Cependant, il y a aussi des risques associés à l’under-sampling, notamment :

Perte d’informations : En réduisant le nombre d’échantillons de la classe majoritaire, vous risquez de perdre des informations potentiellement utiles. Cela peut entraîner une diminution de la capacité du modèle à généraliser et à représenter correctement la classe majoritaire.
Perte de variabilité : L’under-sampling peut réduire la variabilité des données, ce qui peut rendre le modèle moins robuste aux variations naturelles présentes dans les données réelles.

Une autre approche à considérer est l’utilisation de techniques d’ensemble, comme le sous-échantillonnage avec rééchantillonnage bootstrap (Bootstrap Under-Sampling, BUS), qui combine l’under-sampling avec la génération d’échantillons synthétiques. Cela peut aider à prévenir la perte d’informations tout en équilibrant les classes.

Techniques d’ensembles

Les techniques d’ensemble combinent l’under-sampling et la génération d’échantillons synthétiques.
Les risques de cette méthode combinent, logiquement, ceux des deux précédentes.
Pour atténuer ces risques, il est important de surveiller attentivement les performances du modèle sur des données réelles et de valider les résultats avec des métriques d’évaluation appropriées.

Exemple python : Fichier Python

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from imblearn.over_sampling import ADASYN
from imblearn.under_sampling import RandomUnderSampler
from imblearn.combine import SMOTEENN

# Création du jeu de données déséquilibré
X, y = make_classification(n_samples=300, n_features=2, n_informative=2, n_redundant=0, n_classes=3, n_clusters_per_class=1, weights=[0.8, 0.15, 0.05], random_state=42)
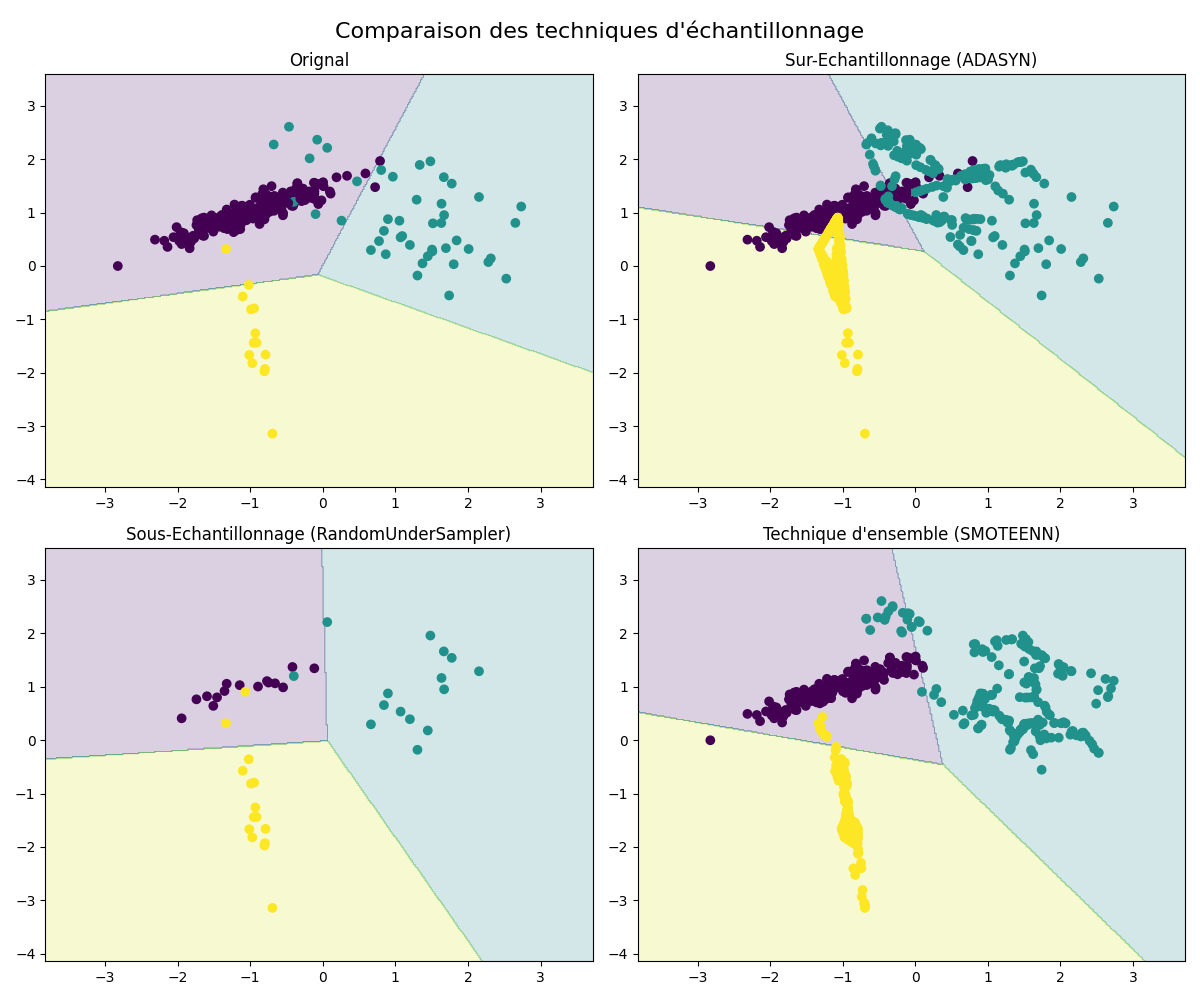
datasets = [{"title": "Orignal", "x": X, "y": y}]

# Oversampling avec ADASYN
ada = ADASYN(random_state=42)
X_ada, y_ada = ada.fit_resample(X, y)
datasets.append({"title": "Sur-Echantillonnage (ADASYN)", "x": X_ada, "y": y_ada})

# Undersampling avec RandomUnderSampler
rus = RandomUnderSampler(random_state=42)
X_rus, y_rus = rus.fit_resample(X, y)
datasets.append({"title": "Sous-Echantillonnage (RandomUnderSampler)", "x": X_rus, "y": y_rus})

# Ensemble avec SMOTEENN
smn = SMOTEENN(random_state=42)
X_smn, y_smn = smn.fit_resample(X, y)
datasets.append({"title": "Technique d'ensemble (SMOTEENN)", "x": X_smn, "y": y_smn})

# Affichages
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle("Comparaison des techniques d'échantillonnage", fontsize=16)

# Préparation du LDA (pour afficher les zones sur les figures)
lda = LinearDiscriminantAnalysis()
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))

for i in range(4):
    a_i, a_j = i // 2, i % 2
    lda.fit(datasets[i]["x"], datasets[i]["y"])
    Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    axes[a_i, a_j].contourf(xx, yy, Z, alpha=0.2)
    axes[a_i, a_j].scatter(datasets[i]["x"][:, 0], datasets[i]["x"][:, 1], c= datasets[i]["y"])
    axes[a_i, a_j].set_title(datasets[i]["title"])

plt.tight_layout()
plt.show()

Comparaison des techniques d'échantillonnage

Normalisation des données

La normalisation des données consiste à ajuster les valeurs d’un ensemble de données de manière à ce qu’elles soient toutes sur la même échelle ou à respecter une certaine distribution. Cela permet de rendre les données comparables entre elles et de les préparer pour des analyses ou des modélisations ultérieures. Ces techniques de normalisation sont largement utilisées dans le prétraitement des données pour garantir que les variables sont comparables et pour améliorer les performances des modèles d’apprentissage automatique en réduisant l’impact des différences d’échelle entre les caractéristiques. En simplifiant, la normalisation des données consiste à mettre les données sur un pied d’égalité.

La normalisation des données présente plusieurs avantages :

Élimination des différences d’échelle : La normalisation permet de ramener les données à une échelle comparable, ce qui facilite la comparaison et le calcul de similarité entre les variables.
Prévention des biais : Certains algorithmes d’apprentissage automatique, tels que les méthodes basées sur la distance, peuvent être biaisés par des variables avec une grande amplitude de valeurs. La normalisation permet d’éviter ce problème en réduisant l’impact des variables à grande échelle.
Accélération de la convergence : Dans les algorithmes d’optimisation, la normalisation peut accélérer la convergence en rendant la surface de l’objectif plus régulière et moins sensible aux différences d’échelle.
Réduction de la sensibilité aux valeurs aberrantes : Certaines techniques de normalisation, comme la normalisation robuste, sont moins sensibles aux valeurs aberrantes, ce qui peut améliorer la stabilité des modèles d’apprentissage automatique.

Il existe plusieurs méthodes de normalisations, les plus courantes sont les suivantes : Normalisation min-max (mise à l’échelle), Normalisation z-score (standardisation), Normalisation par décimales, Normalisation robuste…

En général, le choix de la technique de normalisation dépend du contexte et de la nature des données. Il est recommandé d’expérimenter différentes approches et de surveiller l’impact sur les performances du modèle pour prendre la décision la plus appropriée.

Normalisation min-max (mise à l’échelle)

Cette technique redimensionne les données pour les ramener dans une plage spécifique, généralement entre 0 et 1. La formule utilisée est la suivante :

\[X_n = \frac{X-X_{min}}{X_{max}-X_{min}}\]

Où \(X\) représente la valeur originale, \(X_n\) est la valeur normalisée, \(X_{min}\) est la valeur minimale de l’ensemble de données et \(X_{min}\) est la valeur maximale.

Cette normalisation à un inconvénient majeur qui est la Sensibilité aux valeurs aberrantes : Si l’ensemble de données contient des valeurs aberrantes, la normalisation min-max peut comprimer la plage utile des données en 0-1, ce qui peut réduire les différences entre les autres valeurs.

Normalisation z-score (standardisation)

Cette technique transforme les données de sorte qu’elles aient une moyenne de 0 et un écart type de 1. La formule utilisée est la suivante :

\[X_n = \frac{X-\mu}{\sigma}\]

Où \(X\) représente la valeur originale, \(X_n\) est la valeur normalisée, \(\mu\) est la moyenne de l’ensemble de données et \(\sigma\) est l’écart type.

Cette normalisation à un inconvénient majeur qui est la Distorsion des distributions : La normalisation z-score peut modifier la forme des distributions originales, car elle transforme les valeurs en fonction de la moyenne et de l’écart type. Cela peut être problématique si certaines méthodes d’apprentissage automatique supposent une distribution spécifique des données.

Normalisation par décimales

Cette technique consiste à normaliser les données en les déplaçant vers l’intervalle [0,1] à l’aide des décimales. Par exemple, si les valeurs originales sont dans la plage [1000, 2000], elles peuvent être normalisées en les divisant toutes par 10000 pour les ramener dans la plage [0.1, 0.2].

Cette normalisation à un inconvénient majeur qui est la Perte de précision : Si les valeurs originales sont des nombres à virgule très précis, la normalisation par décimales peut entraîner une perte de précision en divisant toutes les valeurs par un grand nombre.

Normalisation robuste

Cette technique est similaire à la normalisation z-score, mais utilise la médiane et le score interquartile plutôt que la moyenne et l’écart type pour rendre la normalisation moins sensible aux valeurs aberrantes.

\[X_n = \frac{X-\text{Mediane}}{\text{IQR}}\]