Sélection de caractéristiques
- Contexte
- Sélectionner des features
- Réduire le nombre de features
- Réduction du nombre de dimensions par Analyse en composantes principales (PCA)
Avant-propos : Il n’existe pas de solution miracle pouvant réduire le nombre de caractéristiques (features) d’un jeu de donnée. Il existe plusieurs méthodes ayant chacunes ses avantages et inconvénients.
Contexte
Description
Sur cette page nous prendrons un exemple (pseudo-fictif) pour expliquer la méthodologie de sélection de features depuis des données brutes. Dans notre exemple, nous souhaitons estimer l’émotion principale que ressent une personne comme dans la série The Big Bang Theory.

Contrairement à la série qui possède une machine magique permettant de donner les réponses, nous partons de zéro. Nous possédons une base de données de données physiologiques (EEG, ECG, Rythme Cardiaque, Vidéo du visage de la personne, Respiration…) de plusieurs personnes. Le temps de ces enregistrements est découpé en segments avec pour chaque segemnt l’émotion principale de la personne (joie, colère, tristesse, surprise, peur…) est indiqué.
Objectif
Le problème donné précédemment est un soucis de classification, il faut donc entrainer un classifieur avec des échantillons et le tester sur de nouveaux échantillons pour vérifier si le classifieur est capable de faire correctement la distinction entre les états émotionnels.
Problèmes
Nous n’avons aucun apriori sur ce qui permet d’être sûr d’identifier l’état émotionnel d’une personne. Nous avons des tas d’informations pour beaucoup de personnes et beaucoup d’émotions. IL est possible que certaines donnée ne servent à rien et nous ne savons pas encore comment les utiliser.
Fiabilité des résultats
La fiabilité est un point important, j’ai pris l’exemple d’une classification sur un élément concernant un être humain mais chaque humain est différent. Nous avons donc des problèmes supplémentaires :
Puissance Statistique : Avons nous assez de segments dans notre jeu de données brutes ?
Pour valider la pertinence d’un test statistique (un élément est-il plus ou moins inmportant qu’un autre par exemple), nous pouvons utiliser une méthode objective de validation qui serait la puissance statistique.
La puissance statistique mesure la probabilité que le test rejette correctement une hypothèse nulle lorsque l’hypothèse alternative est vraie.
La puissance statistique dépend de plusieurs facteurs, tels que la taille de l’échantillon (notre nombre de segments), le niveau de signification choisi (différence par rapport au hasard), la variabilité des données et l’ampleur de l’effet recherché (par exemple 90 % de succès de détection). En règle générale, plus la taille de l’échantillon est grande, plus la puissance statistique est élevée, car cela permet une meilleure détection des différences ou des effets réels.
La puissance statistique est souvent exprimée en pourcentage, il est souvent difficile d’atteindre une puissance de 100%, mais il est généralement souhaitable d’avoir une puissance statistique élevée, idéalement supérieure à 80%, pour minimiser les risques de conclure à tort qu’il n’y a pas de différence ou d’effet.
où \(\text{Puissance statistique}\) est la probabilité de rejeter l’hypothèse nulle \(H_0\) lorsque l’hypothèse alternative \(H_1\) est vraie, \(\beta\) est la probabilité d’erreur de type II (ne pas rejeter \(H_0\) alors que \(H_0\) est fausse). \(P(\text{Rejeter } H_0 \mid H_0 \text{ est vrai})\) est la probabilité de rejeter \(H_0\) lorsque \(H_0\) est vraie, également appelée taille de l’effet.
Généralisation : Ces personnes sont elles représentatives
Si nous avons les données de personnes qui ont toutes le même age, venant d’une ville précise ayant un niveau d’études identique, d’un genre identique…
Toutes ces informations peuvent influer sur la généralisation de notre machine à détecter les émotions. Une mauvaise généralisation est souvent le cas de données récupérées dans la recherche car il est difficile (voir impossible) d’effectuer une étude à travers le monde sur un grand nombre de personnes (ressources humaines et financières manquantes)
Uniformité : Les émotions sont-elles toutes représentées chez tout le monde et en qu’elle proportion. Comme expliqué dans la page précédente (Les risques dans la classification), un déséquilibre entre les différentes classes peut provoquer des biais lors des calculs et entrainer des résultats avantageant fortement l’émotion majoritaire.
Sélectionner des features
Pour commencer, nous allons extraire des features de nos segments. Chaque segment identifié donnera donc un ensemble de features pour notre classification. Par exemple : Nous pouvons étudier la vidéo et sortir une feature (ou plusieurs) permettant d’identifier la forme de la bouche comme pour des smileys (asymétrie, courbe). La fréquence de clignement des yeux, une identification du niveau froncement de narine… Ensuite, l’EEG peut être utilisé en calculer la puissance moyenne du signal sur une bande de fréquence sur chaque électrode.
La quantité de features à extraire n’a potentiellement que peu de limites. Vous pouvez vous concentrer sur une partie d’entre elles grâce à la littérature, essayer d’être le plus exhaustif possible ou mélanger les deux méthodes.
Réduire le nombre de features
Comme dit au tout début, il n’existe pas de solution miracle pouvant réduire le nombre de caractéristiques (features) d’un jeu de donnée. Il existe plusieurs méthodes ayant chacune ses avantages et inconvénients.
Pourquoi réduire le nombre de features
Admettons que nous ayons essayé d’être exhaustifs. Nous avons désormais 4 000 features sur nos échantillons. La première raison à cette réduction du nombre de dimensions est simplement le temps de calcul nécessaire. Dans notre exemple, nous cherchons à avoir une identification en temps réel de l’état émotionnel d’une personne.
De plus, lors d’une classification, il y a un point nommé malédiction de la dimension qui pourrait se résumer par le fait qu’un nombre de dimensions trop élevé réduit la pertinence du résultat et provoque parfois une impossibilité de calcul pour certains classifieurs.
Ensuite, au vu du nombre de segments pour chaque émotion, nous n’avons pu garder que la joie et la tristesse. Suite à ça, nous avions 20 sujets au départ, il ne nous en reste que 15, 5 d’entre eux n’ayant que pas ou très peu de segments pour une de ces deux émotions. Et pour chacune des émotions nous avons en moyenne qu’une cinquantaine de segments. Avant de chercher à généraliser à une classification pour toutes personnes, nous voulons assurer notre résultat pour chaque personne indépendamment (chacune aura sa propre machine à détecter les émotions).
On pourrait dire que pour que le classifieur soit un minimum viable, il nous faut entre 5 et 10 fois plus d’échantillons que de features. Avec 100 échantillons d’entrainement en moyenne pour 4 000 features, nous sommes loin du ratio de 10 qui nous limiterait à 10 features.
Élimination logique
Il convient d’identifier et supprimer les features qui ne sont pas calculables dans notre contexte. Par exemple le ratio d’énergie de fréquences non présente dans notre signal en entrée donnera des divisions par 0. Il est possible que la littérature utilise ces features par moment, mais dans des paradigmes différents (taille de segment différent, donnée physiologique avec une meilleure résolution…).
Calculs indépendants des classes
Ces méthodes ne cherchent pas à différencier une classe d’une autre et se concentrent sur l’ensemble des échantillons
La variance
Le calcul de la variance de chaque feature permet d’identifier celles ayant une variance très faible, car elles contiennent peu d’informations utiles. Elles peuvent dans certains cas être constantes. Un exemple très simple serait d’avoir ajouté l’âge de la personne en feature, mais cette variable ne change jamais.
En revanche, les features ne sont pas forcément comparables et avec des échelles différentes. Il est préférable de les mettre à la même échelle, plusieurs méthodes sont possible comme compresser les données pour les mettre dans l’interval 0, 1. En multipliant la variance par 100, on aura l’équivalent d’un pourcentage de variance sur cet interval.
Une fois le calcul effectué, on peut classer les features par leurs variances et définir d’un seuil à partir duquel, on considère que la variance est trop faible.
La Corrélation
Le calcul de la corrélation entre chaque paire de features permet de mesurer le niveau de relation linéaire entre deux features. Un résultat de \(1\) indiquera une corrélation positive parfaite, \(-1\) une corrélation négative parfaite et \(0\) une absence totale de corrélation linéaire.
Le coefficient de corrélation le plus couramment utilisé est le coefficient de corrélation de Pearson (noté \(r\)). Il est calculé à l’aide de la formule suivante :
Où \(x_i\) et \(y_i\) sont les valeurs individuelles des deux variables, \(\mu_x\) et \(\mu_y\) sont leurs moyennes respectives, \(\sigma_x\) et \(\sigma_y\) sont leurs écarts-types respectifs, et \(n\) est le nombre d’observations.
La corrélation de Pearson est sensible uniquement à la relation linéaire entre les variables et ne capture pas les relations non linéaires. Il existe d’autres mesures de corrélation, telles que la corrélation de rang de Spearman ou la corrélation de rang de Kendall, qui sont utilisées lorsque la relation entre les variables est non linéaire ou que les données sont classées.
Calculs dépendants des classes
Ces méthodes cherchent à différencier une classe d’une autre et se concentrent sur la comparaison d’une classe par rapport à une autre. Le but étant ainsi d’identifier les features les plus importantes lors de la différenciation entre 2 classes.
Test de Student
Le test de Student, également connu sous le nom de test t de Student, est une méthode statistique utilisée pour déterminer si deux échantillons indépendants diffèrent de manière significative l’une de l’autre. Dans le contexte de l’analyse de données avec deux classes, le test de Student peut être utilisé pour évaluer l’importance des features dans la différenciation entre ces deux classes. Il permet de déterminer si les moyennes des features dans chaque classe sont suffisamment différentes pour conclure qu’il existe une relation significative entre ces features et la distinction entre les deux classes. Le test de Student fournit une valeur de test, appelée t-score, ainsi qu’une valeur de p qui représente la probabilité d’observer des différences aussi importantes (ou plus) entre les deux classes par pure chance. Une valeur de p inférieure à un seuil prédéfini (par exemple 0,05) indique une différence statistiquement significative entre les classes pour cette feature.
ANOVA
L’ANOVA (Analyse de la variance) est une autre méthode statistique utilisée pour comparer les moyennes de plusieurs groupes ou classes. Contrairement au test de Student qui compare deux échantillons, l’ANOVA permet de comparer plus de deux groupes. Dans le contexte de l’analyse de données avec deux classes, on peut également utiliser l’ANOVA pour évaluer l’importance des features dans la différenciation entre ces classes. L’ANOVA fournit une valeur de test appelée F-score, ainsi qu’une valeur de p qui indique si les moyennes des features diffèrent de manière significative entre les classes. De la même manière que pour le test de Student, une valeur de p inférieure à un seuil prédéfini indique une différence statistiquement significative entre les classes pour cette feature.
Le t-test et l’ANOVA sont basés sur des hypothèses concernant la distribution des données. L’une de ces hypothèses est l’homoscédasticité, c’est-à-dire que les variances des échantillons ou des groupes sont égales. Cependant, ces tests sont également assez robustes aux violations mineures de cette hypothèse.
test de Mann-Whitney U
Le test de Mann-Whitney U, également connu sous le nom de test de Wilcoxon-Mann-Whitney, est un test statistique non paramétrique utilisé pour déterminer s’il existe une différence significative entre les distributions de deux échantillons indépendants. Dans le contexte de l’analyse de données avec deux classes, le test de Mann-Whitney U peut être utilisé pour évaluer l’importance des features (variables) dans la distinction entre ces deux classes. Il ne fait pas d’hypothèse spécifique sur la distribution des données et est donc plus approprié lorsque les données ne sont pas normalement distribuées. Le test de Mann-Whitney U compare les rangs des observations des deux classes pour chaque feature, fournissant une valeur de test U et une valeur de p qui indique si les distributions des features diffèrent de manière significative entre les deux classes. Une valeur de p inférieure à un seuil prédéfini (par exemple 0,05) indique une différence statistiquement significative entre les classes pour cette feature.
Test de Kruskal-Wallis
Le test de Kruskal-Wallis est un autre test statistique non paramétrique utilisé pour comparer les distributions de plus de deux groupes indépendants. Dans le contexte de l’analyse de données avec plusieurs classes, le test de Kruskal-Wallis peut être utilisé pour évaluer l’importance des features dans la distinction entre ces classes. Il est similaire au test de Mann-Whitney U, mais il généralise la comparaison à plusieurs groupes. Le test de Kruskal-Wallis évalue si les rangs des observations diffèrent de manière significative entre les classes pour chaque feature, fournissant une valeur de test H et une valeur de p. Une valeur de p inférieure à un seuil prédéfini indique une différence statistiquement significative entre les classes pour cette feature.
Réduction du nombre de dimensions par Analyse en composantes principales (PCA)
L’Analyse en Composantes Principales (PCA) est une méthode puissante de réduction de dimensionnalité qui permet de trouver les axes principaux d’une distribution de données en maximisant la variance. En projetant les données sur un espace de dimension inférieure, la PCA permet de simplifier la visualisation et l’analyse des données tout en conservant autant d’informations que possible.
Dans notre exemple fictif, il est important de définir judicieusement le nombre de composantes à utiliser. Nous avons fixé une limite de 10 features, ce qui signifie que nous pouvons choisir jusqu’à 10 composantes principales. Ces composantes sont des combinaisons linéaires des différentes features, potentiellement filtrées par des méthodes préalables.
Cependant, il est également essentiel de prendre en compte le ratio de variance expliquée lors de la sélection du nombre de composantes. Si le ratio de variance expliquée diminue considérablement après l’ajout d’une certaine composante, cela signifie que cette composante apporte moins d’informations utiles. Dans notre exemple, si la première composante explique 40 % de la variance, la deuxième 35 %, et la troisième seulement 1 %, il devient peu utile d’ajouter davantage de composantes. Dans ce cas, il est suffisant de prendre en compte les deux premières composantes pour obtenir une représentation significative des données. Il est également possible de choisir arbitrairement le nombre de composantes necessaire pour atteindre un certain pourcentage de variance (par exemple 80%)
La sélection du nombre de composantes peut être basée sur une compréhension du domaine, une analyse exploratoire des données ou des techniques d’optimisation spécifiques. Il est essentiel de trouver le bon équilibre entre la dimensionnalité réduite et la conservation des informations importantes contenues dans les données.
Exemple python : Fichier Python
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
# Chargement des données d'exemple
print("Chargement du dataset")
dataset = load_digits()
# Réduction de la dimension à 2 en utilisant PCA
print("Calcul du PCA")
pca = PCA()
pca.fit(dataset.data)
X_reduced = pca.transform(dataset.data)
explained_var = pca.explained_variance_ratio_
cumulative_var = np.cumsum(explained_var)
weights = pca.components_.T # Vecteurs de chargement des caractéristiques
# Affichage des résultats
print("Affichages")
fig, ax = plt.subplots(figsize=(8, 5))
scatter = ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=dataset.target, marker='o')
legend = ax.legend(*scatter.legend_elements(), loc="lower left", title="Classes")
ax.add_artist(legend)
ax.set_title("Graphique sur 2 composantes principales")
plt.show()
# Affichage de la variance cumulée
fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(range(1, len(cumulative_var) + 1), cumulative_var, marker='o')
ax.set_xlabel("Nombre de composantes principales")
ax.set_ylabel("Ratio de variance expliquée cumulée")
ax.set_title("Graphique du ratio de variance expliquée")
seuil_plat = 0.001 # Seuil pour définir la planéité de la courbe
for i in range(1, len(cumulative_var)):
x1, x2 = range(i - 1, i + 1)
y1, y2 = cumulative_var[i - 1:i + 1]
pente = (y2 - y1) / (x2 - x1)
if pente < seuil_plat: # dès qu'on passe ce seuil
x_tangente = np.array([0, len(cumulative_var)])
y_tangente = pente * (x_tangente - x1) + y1
ax.plot(x_tangente, y_tangente, linestyle='-', color='red')
ax.vlines(x2, ymin=cumulative_var[0], ymax=1, linestyle='--', color='red')
ax.text(x2, cumulative_var[0], f" N = {x2}", ha='left', va='bottom', color='red')
ax.text(x2, y2 + 0.01, f"Variance = {y2:.3f}", ha='center', va='bottom', color='red')
break
plt.show()
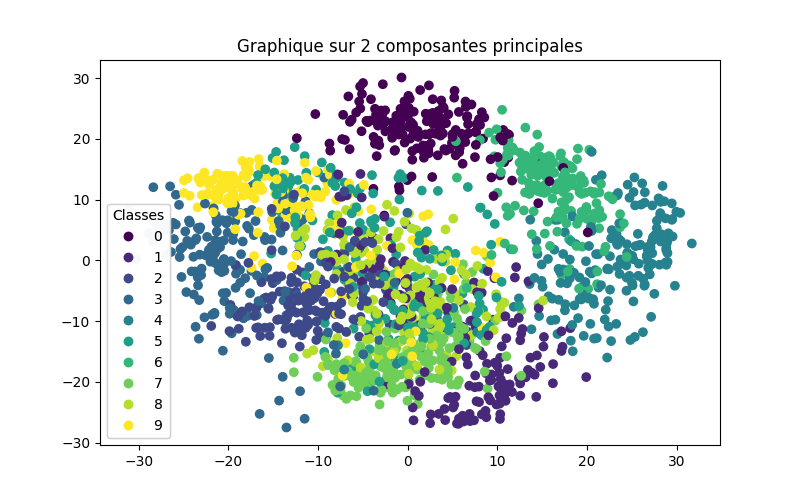
Sur les deux figures précédentes, nous avons affiché les deux premières composantes principales. Nous pouvons observer que l’ensemble du jeu de données est réparti en 10 classes, mais il est difficile de bien séparer les classes uniquement avec ces deux composantes. Cela suggère que ces deux dimensions ne capturent pas suffisamment d’informations pour une classification précise.
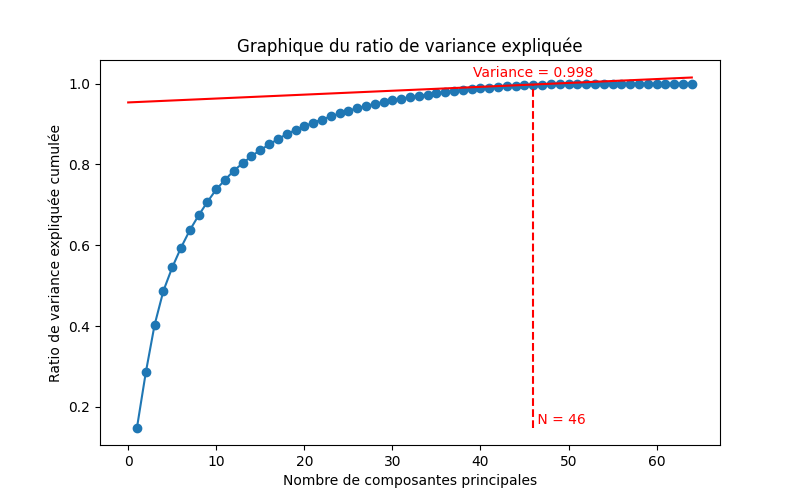
En examinant le graphique du ratio de variance expliquée, nous pouvons constater qu’il y a une augmentation significative de la variance expliquée entre 2 et 3 composantes principales. Cela indique que l’ajout d’une troisième composante permettrait de capturer davantage d’informations pertinentes contenues dans les données.
J’ai tracé la tangente à la courbe lorsque le ratio de variance expliquée atteint un seuil à partir duquel j’estime que l’ajout de composantes devient inutile. Dans ce jeu de données spécifique, nous pouvons voir qu’à partir de 46 composantes, la classification du dataset serait suffisamment performante.
