Géométrie Riemannienne appliquée aux BCI

Base
Géométrie Riemannienne
- Exemple pratique lié au BCI

Sources Principales :

Congedo, Marco and Barachant, Alexandre and Bhatia, Rajendra 2018. Riemannian geometry for EEG-based brain-computer interfaces; a primer and a review. Brain-Computer Interfaces, 4, 155–174. hal-01570120 [pdf]
Yger, Florian and Berar, Maxime and Lotte, Fabien 2017. Riemannian Approaches in Brain-Computer Interfaces: A Review. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 25, 1753–1762. hal-01394253 [pdf]
Congedo, Marco and Afsari, Bijan and Barachant, Alexandre and Moakher Maher 2015. Approximate Joint Diagonalization and Geometric Mean of Symmetric Positive Definite Matrices. PLOS ONE, 10, 25. hal-01149652 [pdf]

Source Bibliothèque Libre : pyRiemann
Ma Bibliothèque C++ Libre : Riemann Geometrie

Base

Définition

La géométrie riemannienne permet l’étude de variétés géométrique et de courbure. Il s’agit de surfaces ou d’objets de plus grande dimension sur lesquels existent des notions d’angle et de longueur, généralisant la géométrie traditionnelle qui se limitait à l’Espace euclidien. Le but principal de la géométrie riemannienne est l’étude des courbures de l’espace et les géodésiques permettant de réoudre les problèmes de plus court chemin.

Variété Riemannienne

Variété Géométrique :
La variété géométrique est la classification d’éléments géométrique : Une courbe est une variété de dimension 1 (en indiquant le déplacement sur la courbe, on a la position), une surface est une variété de dimension 2 (on a besoin de deux coordonnées pour se positionner comme longitude et latitude sur la planète). La variété est indépendante de l’espace utilisé, par exemple une courbe dans un espace 3D est toujours une variété de dimension 1.

Variété topologique :
Les variétés topologiques sont des espaces dans lesquels chaque point a un voisinage homéomorphe à $\mathbb{R}^n$. Pour simplifier, une variété topologique peut être vue comme un espace qui semble localement plat.

Variété Différentielle :
Dotée d’une structure différentielle, également appelée atlas (c’est-à-dire un ensemble de bijections appelées diagrammes entre un ensemble de sous-ensembles de la variété topologique et un ensemble de sous-ensembles ouverts de $\mathbb{R}^n$), la variété topologique devient une variété différentielle. Dans les variétés différentielles, il existe des variétés lisses qui sont des variétés différentielles pour lesquelles les transitions entre les cartes sont lisses. Pour simplifier à nouveau, cette étape a pour but de donner des règles permettant de traduire localement un point de la variété en son approximation linéaire. Ces règles sont locales, mais sur une variété lisse, les règles changent légèrement d’un point à un autre.

Sur chaque point d’une variété différentielle lisse, la notion d’espace tangent peut être définie comme la vitesse des courbes passant par le point. Une variété riemannienne est alors une vraie variété lisse dotée d’un produit interne sur l’espace tangent en chaque point.

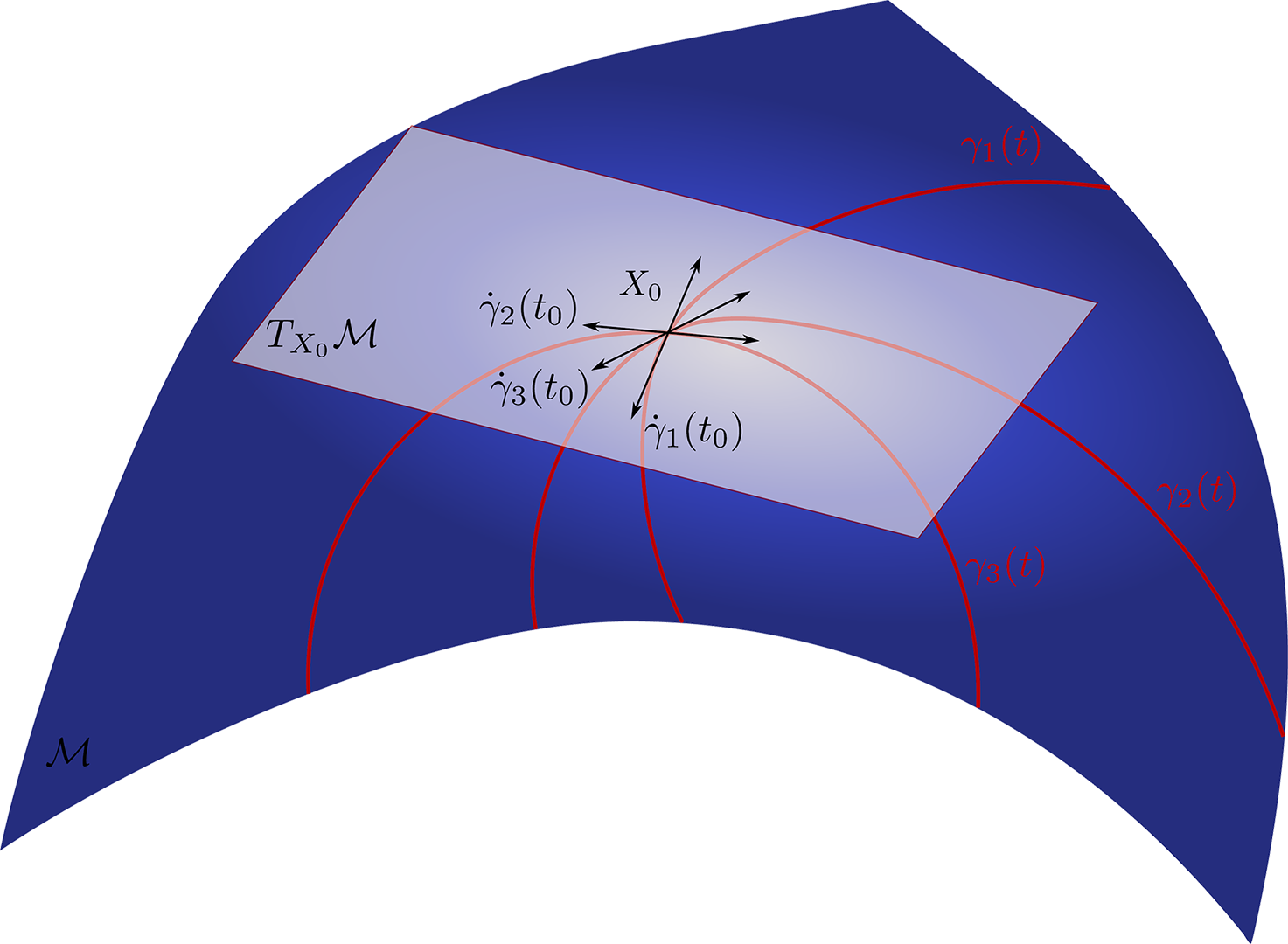
Variété Riemannienne :
une variété riemannienne est une variété différentielle munie d’une structure supplémentaire appelée métrique riemannienne permettant de calculer le produit scalaire de deux vecteurs tangents à la variété en un même point. Cette métrique permet de définir la longueur d’un chemin entre deux points de la variété, puis les géodésiques qui répondent à un problème de plus court chemin.

Pour toute variété riemannienne, il existe une paire de correspondances transportant des points de la variété vers un espace tangent donné et inversement. Plus précisément, le mappage exponentiel transporte un vecteur tangent (c’est-à-dire un point dans un espace tangent) vers la variété et le mappage logarithmique est défini localement pour transporter un point situé au voisinage d’un point dans l’espace tangent défini à cet endroit. En conséquence, les variétés riemanniennes peuvent être localisées approximativement par les espaces euclidiens via leurs espaces tangents, bien que des déformations se produisent pour les points cartographiés loin de l’endroit où le point tangent est défini.

Géodésique :
Une géodésique désigne la généralisation d’une ligne droite sur une surface. En particulier, le chemin le plus court ou un des plus courts chemins, s’il en existe plusieurs, entre deux points d’un espace pourvu d’une métrique est une géodésique. Par exemple, le chemin le plus court sur une sphère est un grand cercle (cercle du diamètre de la sphère).

Métrique

En mathématiques, une métrique (ou distance) est une fonction qui définit une distance entre chaque paire d’éléments d’un ensemble, avec les propriétés suivantes:

Il est positif
il n’est égal à zéro que si les deux éléments sont égaux
Il est symétrique
il obéit à l’inégalité du triangle.

Espace métrique :
Un ensemble doté d’une métrique s’appelle un espace métrique. Par exemple, nous définissons ici l’espace métrique $(S, d)$ comme l’ensemble des nombres réels positifs $S = (0,\infty)$ dotés de la métrique $d$. Selon un principe de Maurice Fréchet, chaque métrique dans cet espace métrique conduit au concept de moyenne tel qu’il suit:

Approche variationnelle de Fréchet (cas monodimensionnel)
Soit $(S,d)$ l’espace métrique des nombres réels positifs dotés de la métrique $d$ et $\{c_1, \dots, c_K\}$ soit un ensemble de $K$ points en son sein. La moyenne de l’ensemble $\{c_1, \dots, c_K\}$ est un point $x$ minimisant la dispersion $\frac{1}{K} \sum_{k=1}^K{d^2(x,c_k)}$.

La métrique la plus connue sur S est la distance euclidienne “habituelle” :

\[d_E(a,b) = \lvert a - b \rvert\]

la moyenne euclidienne correspondante d’un ensemble de points $\{c_1, \dots, c_K\}$ est le point $m$ qui résout la minimisation :

\[\arg_m \min \frac{1}{K} \sum_{k=1}^K{d_E^2(m,c_k)} = \arg_m \min \frac{1}{K} \sum_{k=1}^K{\lvert m - c_k \rvert^2}\]

Cela se révèle être la moyenne arithmétique habituelle :

\[\frac{1}{K} \sum_{k=1}^K{c_k}\]

Ainsi, la moyenne euclidienne est le point minimisant la variance de l’échantillon, la dispersion de l’ensemble autour de la moyenne en fonction de la distance euclidienne.

Distance et Moyenne Géométrique

En BCI, la distance euclidienne ne fournit pas de bonne performance. À l’instar des décibels pour le son, on utilise le logarithme pour avoir la distance Log-Euclidienne (Log-Euclidian) appelée Distance Géométrique (ou Hyperbolique) sur S, définie par :

\[d_G(a,b) = \left\lvert \log{a} - \log{b} \right\rvert = \left\lvert \log{\frac{a}{b}} \right\rvert\]

En statistique, si $a$ et $b$ sont deux variances d’échantillon, leur ratio est la statistique habituelle de Snedecor $F$ pour tester l’égalité de deux variances et le log de ce ratio correspond à la distribution générale de Fisher $z$. Contrairement à la distance euclidienne, la distance géométrique bénéficie de l’invariance d’échelle et l’invariance sous inversion.

\[d_G(xa,xb) = d_G(a,b), ~\forall~ a, b, x > 0 \\ d_G(a^{-1},b^{-1}) = d_G(a,b), ~\forall~ a, b > 0\]

La moyenne de Fréchet des $K$ points $\{c_1, \dots, c_K\}$ correspondant à la distance géométrique est le point $g$ qui résout le problème de minimisation :

\[\arg_g \min \frac{1}{K} \sum_{k=1}^K{d_G^2(g,c_k)} = \arg_g \min \frac{1}{K} \sum_{k=1}^K{\left\lvert \log{g} - \log{c_k} \right\rvert^2}\]

Cela se révèle être une autre moyenne célèbre de Pythagore, la moyenne géométrique:

\[g = \sqrt[K]{c_1 \cdot c_2 \cdot ~...~ \cdot c_k } = \exp{\left( \frac{1}{K} \sum_{k=1}^K{\log{c_k}} \right)}\]

Cette moyenne est plus adaptée aux variables ayant une distribution asymétrique ou possédant des valeurs aberrantes.

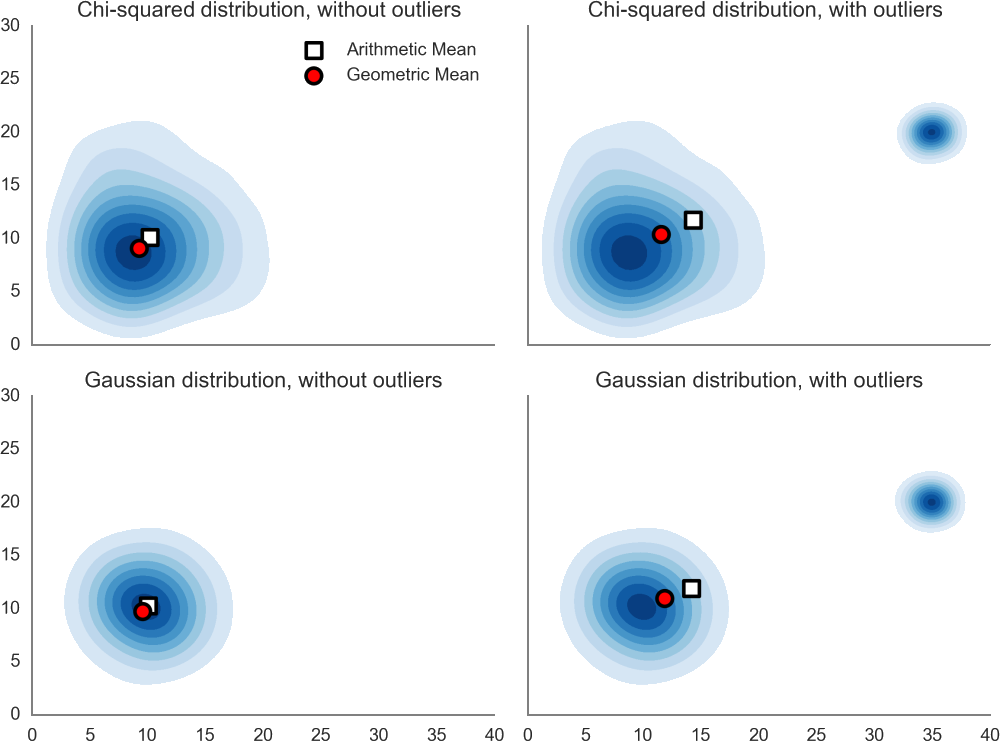
Différence entre moyenne arithmétique et géométrique — Moyennes arithmétiques et géométriques. Isodensités empiriques des distributions du Chi-carré (10 degrés de liberté, rangée du haut) et gaussiennes (rangée du bas), sans (colonne de gauche) et avec des valeurs aberrantes (colonne de droite). *Source : [1]*

Géométrie Riemannienne

Nota Bene :

$N$ : Nombre de dimensions	$K$ : Nombre d’échantillons	$C_i$ : Point $i$, i.e. Matrice de covariance
$\delta$ : Métrique	$\delta_E$ : Métrique Euclidienne	$\delta_G$ : Métrique Géométrique
$\mu$ : Moyenne	$M$ : Moyenne Arithmétique	$G$ : Moyenne Géométrique

Métrique Riemannienne :
La métrique riemannienne sur les matrices symétriques positives est une généralisation à $N$ dimensions de la distance géométrique.

Exemple pratique lié au BCI

Définition de l’espace

Avec deux électrodes (C3 et C4 par exemple), on a :

$N=2$ (2 Dimensions)
$x_1(t)$ et $x_2(t)$ les deux enregistrements (C3 et C4)
$x_{1k}$ et $x_{2k}$ la $k^{eme}$ fenêtre d’analyse temporelle.
$C_k$ la matrice de covariance telle que :
$C_k = \begin{pmatrix} \operatorname{Var}{\left(x_{1k} \right)} & \operatorname{Cov}{\left(x_{1k},x_{2k} \right)} \\ \operatorname{Cov}{\left(x_{2k},x_{1k} \right)} & \operatorname{Var}{\left(x_{2k} \right)} \end{pmatrix}$
- Comme $\operatorname{Cov}{\left(x_{1k},x_{2k} \right)}=\operatorname{Cov}{\left(x_{2k},x_{1k} \right)}$ la matrice de covariance $C_k$ est symétrique et possède $\left(N\left(N+1\right)\right)/2$ éléments
- $C_k$ peut s’écrire sous la forme d’un vecteur 3D
  \[C_k=\begin{bmatrix} \operatorname{Var}{\left(x_{1k}\right)} \\ \operatorname{Var}{\left(x_{2k}\right)} \\ \operatorname{Cov}{\left(x_{1k},x_{2k}\right)} \end{bmatrix}\]

Du fait de l’inégalité de Cauchy-Schwartz, on a :

\[\left\lvert\operatorname{Cov}{\left(x_{1k},x_{2k}\right)}\right\rvert^2 \leq \operatorname{Var}{\left(x_{1k}\right)} \operatorname{Var}{\left(x_{2k}\right)}\]

Donc tout point est à l’intérieur d’un Cône convexe symétrique. Toute matrice définie positive symétrique se situe à l’intérieur d’un cône ouvert en raison de l’inégalité de Cauchy-Schwarz. Lorsque le point touche la frontière du cône, l’inégalité devient une égalité et la matrice n’est plus définie positive.

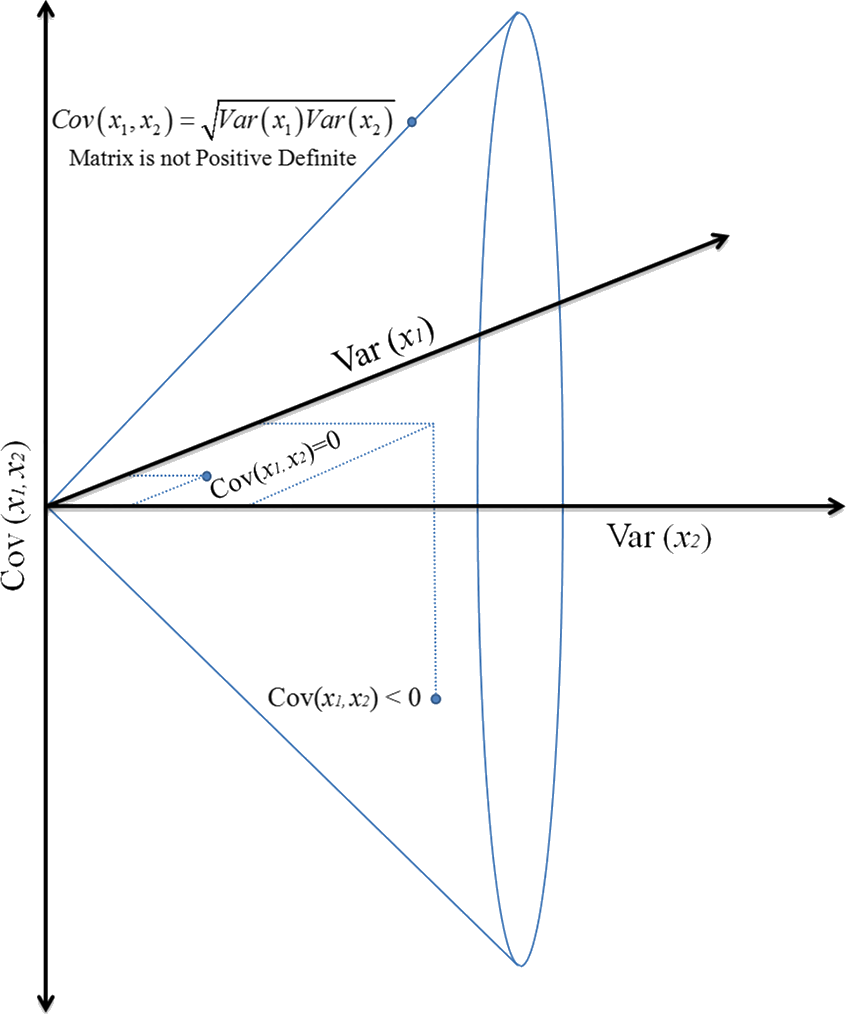
Cône convexe symétrique des matrices SPD — Matrices définies positives symétriques, par ex. matrices de covariance, sont contraintes par leur symétrie, la positivité stricte des éléments diagonaux (variance) et les inégalités de Cauchy-Schwarz délimitant la valeur absolue des éléments hors diagonale: $\left\lvert\operatorname{Cov}\left(x_i,w_j\right)\right\rvert \leq \sqrt{\operatorname{Var}{\left(x_i\right)}\operatorname{Var}{\left(x_j\right)}},~ \forall i,j \in \{1, \dots N\}$ . Cette topologie est facilement visualisable dans le cas de matrices 2x2; toute matrice de covariance 2x2 peut être vue comme un point dans l'espace euclidien 3D, avec deux coordonnées données par les deux variances (éléments diagonaux) et la troisième coordonnée donnée par la covariance (l'un ou l'autre des éléments non diagonaux). Par construction, une matrice de covariance doit rester dans les limites du cône. Dès que le point touche la limite du cône, l'inégalité devient égalité et la matrice n'est plus définie positive. *Source : [1]*

En termes électrophysiologiques, la réalisation $C_k$ se déplace le long des trois coordonnées lorsque l’énergie (variance) de l’une des deux électrodes change ou lorsque la synchronisation de phase et/ou la co-modulation d’amplitude entre le signal capturé au niveau des deux électrodes change. Plus deux points s’éloignent l’un de l’autre le long de ces coordonnées, plus ils occuperont des régions séparées dans le cône.
Pour toute dimension supérieure N, le cône deviendra un hypercône, mais cela s’applique de la même manière.

Application de la distance géométrique

L’espace des matrices symétriques $N \times N$ est un espace linéaire de dimension $N\left(N + 1\right) / 2$. Il a un produit intérieur naturel (produit scalaire) donné par $\langle A,B \rangle = \operatorname{tr}{\left(AB\right)}$ et la norme euclidienne associée $\lVert A \rVert_2$, définie par :

\[\lVert A\rVert_2^2 = \operatorname{tr}{A^2} = \sum_n{\lambda_n\left(A\right)^2}\]

où $\lambda_n\left(A\right)^2$ sont les $N$ Les valeurs propres de A et $\operatorname{tr}$ est l’opérateur de trace.

Si la matrice A a des éléments $a_{ij}$, alors :

\[\lVert A \rVert_2^2 = \sum_{i,j=1}^N{\left\lvert A \right\rvert^2}\]

Donc, $\lVert A\rVert_2$ est une extension naturelle aux matrices de la norme euclidienne sur les vecteurs. Le cône des matrices positives est un sous-ensemble de matrices symétriques et hérite naturellement de cette norme euclidienne.

Cela peut être satisfaisant pour certains problèmes, mais présente plusieurs inconvénients dans le contexte BCI, même dans le cas le plus simple monodimensionnel. Heureusement, une autre norme et une distance associée provenant de la géométrie riemannienne s’avèrent être la bonne.

L’ensemble $S_{++} (N)$ des matrices positives $N \times N$ est une variété différentiable. C’est-à-dire que chaque petit voisinage autour d’un point P “ressemble” à l’espace euclidien de matrices symétriques, dont il est un ensemble ouvert. L’espace de toutes les matrices symétriques à n’importe quel point de base du collecteur s’appelle l’espace tangent. La géométrie riemannienne commence par équiper avec un produit interne chaque espace tangent, de manière à ce que la métrique résultante varie progressivement d’un point à un autre. Dans ce cas, le produit intérieur en un point donné $P$ est :

\[\langle A,B \rangle_P = \operatorname{tr}{\left( P^{-1}AP^{-1}B \right)}\]

La norme associée est alors $\lVert A \rVert_{2,P}$, donnée par :

\[\lVert A \rVert_{2,P}^2 = \left\lVert P^{-1}A \right\rVert_2^2 = \left\lVert P^{-1/2}AP^{-1/2} \right\rVert_2^2\]

Lorsque $P=I$, la matrice d’identité, cela se réduit à la norme $\lVert A \rVert_2$ introduite précédemment.

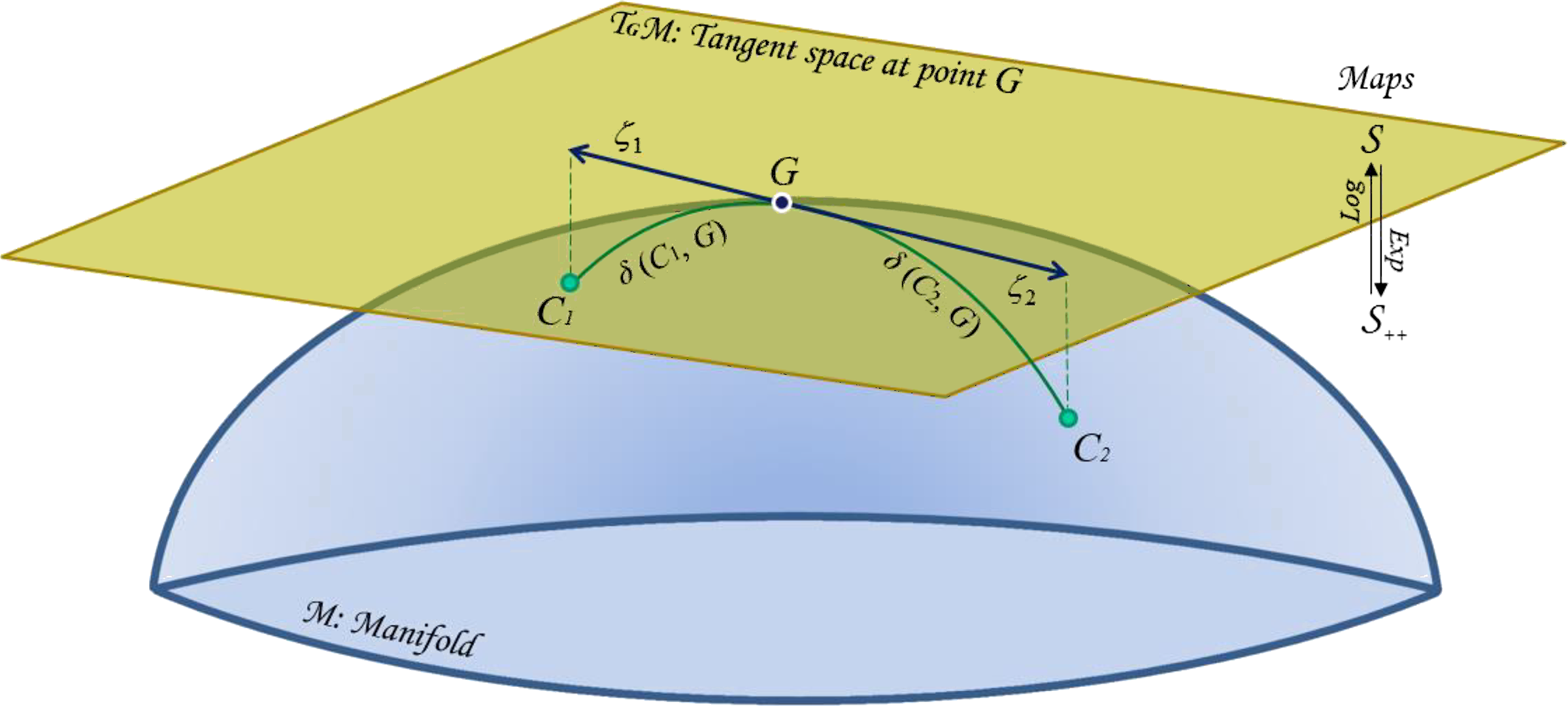
Représentation schématique de la variété symétrique à matrice définie positive. — Représentation schématique de la variété des matrices symétrique définie positive, de la moyenne géométrique $G$ de deux points et de l'espace tangent en $G$ . Considérons deux points (par exemple, deux matrices de covariance) $C_1$ et $C_2$ sur $\mathcal{M}$ . La moyenne géométrique de ces points est le milieu de la géodésique reliant $C_1$ et $C_2$ , c’est-à-dire qu’elle minimise la somme des deux distances au carré $\delta^2(C_1,G)+\delta^2(C_2,G)$ . Construisons maintenant l'espace tangent $\mathcal{T}_G\mathcal{M}$ en $G$ . Il existe un et un seul vecteur tangent $\zeta_1$ (respectivement $\zeta_1$ ) correspondant à la géodésique partant de $G$ et arrivant en $C_1$ (respectivement $C_2$ ) sur la variété. La carte de l'espace tangent (matrices symétriques $S$ ) à la variété (matrices définies positives symétriques $S_{++}$ ) est une carte exponentielle. La carte inverse de la variété vers l'espace tangent est une carte logarithmique. *Source : [1]*

Calcul de la distance géométrique

On calcule la longueur de toute courbe dans l’espace $S_{++}(N)$ à l’aide du produit interne sur l’espace tangent. Étant donné deux points (Matrices de Covariance) quelconques $C_1$ et $C_2$ en $S_{++}(N)$, plusieurs courbes pourraient les traverser. La variété des matrices positives avec un produit intérieur sur l’espace tangent possède, pour deux points quelconques, une longueur minimale appelée géodésique. Elle est donnée par :

\[\delta_G\left(C_1,C_2\right) = \left\lVert \operatorname{Log}{\left( C_1^{-1/2}C_2C_1^{-1/2}\right)} \right\rVert_F = \sqrt{\sum_{n=1}^N{\log^2{\lambda_n}}}\]

Définition de la norme de Frobenius ici : $\left\lVert A \right\rVert_F$

Où $\lambda_n$ sont les $N$ valeurs propres de la matrice $C_1^{-1/2}C_2C_1^{-1/2}$ ou, de manière équivalente, de la matrice $C_1^{-1}C_2$ et où, dans les deux expressions, les indices 1 et 2 peuvent être permutés (cette distance est symétrique). Dans le cas où $N = 1$, cela se réduit à la distance géométrique entre les nombres réels positifs.

Remarque

La définition de distance en tant que longueur d’une géodésique garantit qu’elle possède toutes les propriétés d’une fonction de distance. Il possède plusieurs propriétés supplémentaires intéressantes, dont certaines sont importantes pour son utilisation dans les BCI.

La distance est invariante sous toute congruence, c’est-à-dire :

\[\delta_G\left( XC_1X^{\mathsf{T}},XC_2X^{\mathsf{T}} \right) = \delta_G\left( C_1,C_2 \right)\]

elle est également invariante sous inversion, c’est-à-dire

\[\delta_G\left( C_1^{-1},C_2^{-1} \right) = \delta_G\left( C_1,C_2 \right)\]

Ces deux propriétés sont des extensions simples des équations de la partie Distance et Moyenne Géométrique et sont déterminantes pour la robustesse des décodeurs BCI riemanniens.

Calcul de la moyenne géométrique

Approche variationnelle de Fréchet (cas général)
Soit $(S_{++}(N),\delta)$ l’espace métrique des matrices positives dotées de la métrique $\delta$ et de $\{C_1, \dots, C_K\}$ un ensemble de $K$ points. La moyenne de l’ensemble $\{C_1, \dots, C_K\}$ est un point $X$ minimisant la dispersion $\frac{1}{K} \sum_{k=1}^K{\delta^2(X,C_k)}$.

La condition de minimisation de la dispersion existe et il est unique. En fait, ce n’est peut-être pas le cas. Par exemple, à la surface d’une sphère avec sa distance habituelle, deux points antipodaux ont une infinité de “moyennes”, en raison du fait qu’il n’existe pas de géodésique dans ce cas. À titre d’exemple, prenons les points comme les deux pôles: tous les points de l’équateur sont également des candidats raisonnables pour une “moyenne”.

Encore une fois, la moyenne arithmétique $M=\frac{1}{K}\sum_{k=1}^K{C_k}$ est la minimisation de la dispersion en fonction de la distance euclidienne, c’est-à-dire :

\[\arg_M \min \frac{1}{K} \sum_{k=1}^K{\delta_E^2\left(C_k,M\right)} = \frac{1}{K} \sum_{k=1}^K{\left\lVert C_k - M \right\rVert_F^2}\]

Avec la distance géométrique, nous avons :

\[\arg_G \min \frac{1}{K} \sum_{k=1}^K{\delta_G^2\left(C_k,G\right)}\]

La métrique riemannienne $\delta_G$ a plusieurs propriétés intéressantes garantissant que $G$ ainsi défini existe et est unique. $G$ est diversement appelé moyenne de Cartan, Karcher, Fréchet, Riemannienne ou géométrique, ainsi que le centre de masse de $\{C_1, \dots, C_K\}$.

Remarque

Les propriétés d’invariance de la distance Riemannienne confèrent à la moyenne géométrique $G$ l’invariance de congruence, c’est-à-dire :

\[G\left( XC_1X^{\mathsf{T}}, \dots, XC_kX^{\mathsf{T}} \right) = XG\left( C_1, \dots, C_k \right)X^{\mathsf{T}}\]

Pour tout X inversible, elle a également la dualité de soi (self-duality) c’est-à-dire :

\[G\left( C_1^{-1}, \dots, C_k^{-1} \right) = \left(G\left( C_1, \dots, C_k \right)\right)^{-1}\]

La moyenne arithmétique possède l’invariance de congruence mais pas la dualité de soi.
Une autre propriété importante est l’identité du déterminant : le déterminant de la moyenne géométrique $G\left( C_1, \dots, C_k \right)$ est égal à la moyenne géométrique des déterminants de $C_1, \dots, C_k$. Cela contraste avec la moyenne arithmétique, où le déterminant de $1/2\left(C_1 + C_2\right)$ peut être plus grand que le déterminant de $C_1$ et de $C_2$.

Lorsque $K>2$, aucune expression sous forme fermée de la moyenne géométrique n’est connue. Une caractérisation utile de la moyenne géométrique est la solution unique de l’équation matricielle non linéaire :

\[\frac{1}{K} \sum_{k=1}^K{\operatorname{Log}{\left(G^{-1/2} C_k G^{-1/2}\right)}} = 0\]

Thibaut Monseigne

Ingénieur Recherche et Développement en Interface Cerveau-Machine.

\(N\) : Nombre de dimensions	\(K\) : Nombre d’échantillons	\(C_i\) : Point \(i\), i.e. Matrice de covariance
\(\delta\) : Métrique	\(\delta_E\) : Métrique Euclidienne	\(\delta_G\) : Métrique Géométrique
\(\mu\) : Moyenne	\(M\) : Moyenne Arithmétique	\(G\) : Moyenne Géométrique

Géométrie Riemannienne appliquée aux BCI

Base

Définition

Variété Riemannienne

Métrique

Distance et Moyenne Géométrique

Géométrie Riemannienne

Exemple pratique lié au BCI

Définition de l’espace

Application de la distance géométrique

Calcul de la distance géométrique

Remarque

Calcul de la moyenne géométrique

Remarque

Thibaut Monseigne

Recent post