Normalisation de la distribution d'un signal
Description
La normalité dans le contexte de la distribution d’un signal fait référence à une distribution qui suit une loi normale, également appelée distribution gaussienne. Une distribution normale est caractérisée par une forme symétrique en forme de cloche, où la majorité des observations se trouvent près de la moyenne et la dispersion décroît à mesure que l’on s’éloigne de la moyenne.
La normalité peut être utile dans différentes applications pour plusieurs raisons :
- Tests statistiques : De nombreux tests statistiques et méthodes d’inférence sont basés sur l’hypothèse que les données suivent une distribution normale. Par conséquent, si les données ne sont pas normalement distribuées, l’application de ces tests peut être invalide ou donner des résultats erronés.
- Modélisation et prévision : La normalité peut simplifier la modélisation des données et faciliter la prévision future. Les modèles statistiques, tels que la régression linéaire ou l’analyse de séries temporelles, supposent souvent que les résidus ou les erreurs suivent une distribution normale.
- Méthodes paramétriques : Les méthodes paramétriques, telles que l’estimation des paramètres ou les intervalles de confiance, peuvent être plus fiables et précises lorsque les données suivent une distribution normale. Dans ces méthodes, des hypothèses sur la distribution des données sont nécessaires, et la normalité facilite souvent les calculs et l’interprétation des résultats.
- Tests d’hypothèses : Certains tests d’hypothèses, tels que le test t de Student, supposent également une distribution normale des données pour être valides. En s’assurant que les données sont normalement distribuées, on peut garantir la validité de ces tests et prendre des décisions basées sur des résultats statistiquement fiables.
Cependant, il est important de noter que dans de nombreuses situations réelles, les données peuvent ne pas être strictement normales. Dans certains cas, des transformations appropriées peuvent être appliquées pour rendre les données plus proches d’une distribution normale, permettant ainsi l’application des méthodes statistiques basées sur cette hypothèse. Des techniques telles que les transformations logarithmiques, les transformations de Box-Cox ou les méthodes de normalisation peuvent être utilisées à cet effet.
Méthodes
Transformation logarithmique
Définition : La transformation logarithmique consiste à prendre le logarithme des valeurs d’un signal.
Avantages : Cette transformation peut être utile lorsque les données ont une distribution fortement asymétrique positive. Elle peut réduire la variation et rendre la distribution plus symétrique, se rapprochant potentiellement d’une distribution normale.
Inconvénients : La transformation logarithmique n’est pas applicable lorsque les données contiennent des valeurs négatives ou nulles, car le logarithme de ces valeurs n’est pas défini.
Transformation exponentielle
Définition : La transformation exponentielle consiste à prendre l’exponentielle des valeurs d’un signal.
Avantages : Cette transformation peut être utilisée pour inverser une transformation logarithmique et ramener les données à leur échelle d’origine. Elle peut également être utile lorsque les données ont une distribution fortement asymétrique négative.
Inconvénients : Comme pour la transformation logarithmique, la transformation exponentielle n’est pas applicable lorsque les données contiennent des valeurs négatives.
Transformation de Box-Cox
Définition : La transformation de Box-Cox est une méthode qui vise à trouver la transformation optimale d’un signal en utilisant une famille de transformations paramétriques.
Avantages : La transformation de Box-Cox peut être utilisée pour normaliser les données en trouvant la meilleure transformation paramétrique pour rendre la distribution aussi proche que possible d’une distribution normale. Elle peut gérer une variété de distributions asymétriques.
Inconvénients : La transformation de Box-Cox nécessite l’estimation du paramètre optimal de transformation, ce qui peut être plus complexe. De plus, elle peut ne pas fonctionner efficacement si les données contiennent des valeurs nulles ou négatives.
Standardisation
Définition : La standardisation (ou z-score) consiste à soustraire la moyenne des données et à diviser par l’écart-type.
Avantages : La standardisation permet de transformer les données pour qu’elles aient une moyenne de zéro et un écart-type de 1. Cela peut faciliter la comparaison des données et la mise en évidence des valeurs atypiques.
Inconvénients : La standardisation ne modifie pas la distribution des données pour les rendre normales, elle se concentre plutôt sur la mise à l’échelle des données. Elle peut également être sensible aux valeurs extrêmes.
Transformation des rangs
Définition : La transformation des rangs assigne à chaque valeur son rang dans l’ensemble des données. Les valeurs sont triées puis numérotées de 1 à N.
Suivant la méthode, les valeurs identiques peuvent avoir le rang moyen, minimum ou maximum de ces valeurs.
Avantages : La transformation des rangs permet de transformer les données en une distribution uniforme où chaque valeur a un rang spécifique. Elle peut être utile lorsque les données ont une distribution très asymétrique.
Inconvénients : La transformation des rangs ne modifie pas la forme de la distribution, elle redistribue simplement les valeurs. Elle peut également être affectée par des valeurs identiques qui reçoivent le même rang.
Transformation de puissance
Définition : La transformation de puissance consiste à appliquer une puissance aux valeurs d’un signal, comme la racine carrée ou la puissance cubique.
Où \(n\) peut être n’importe quel nombre (puissance cubique si \(n=3\), racine carrée si \(n=\frac{1}{2}\)…).
Avantages : La transformation de puissance peut aider à réduire l’asymétrie et à rendre la distribution plus symétrique, en se rapprochant potentiellement d’une distribution normale.
Inconvénients : La transformation de puissance peut modifier considérablement la distribution des données, ce qui peut rendre l’interprétation plus difficile. De plus, le choix de la puissance doit être fait avec soin pour éviter des effets indésirables.
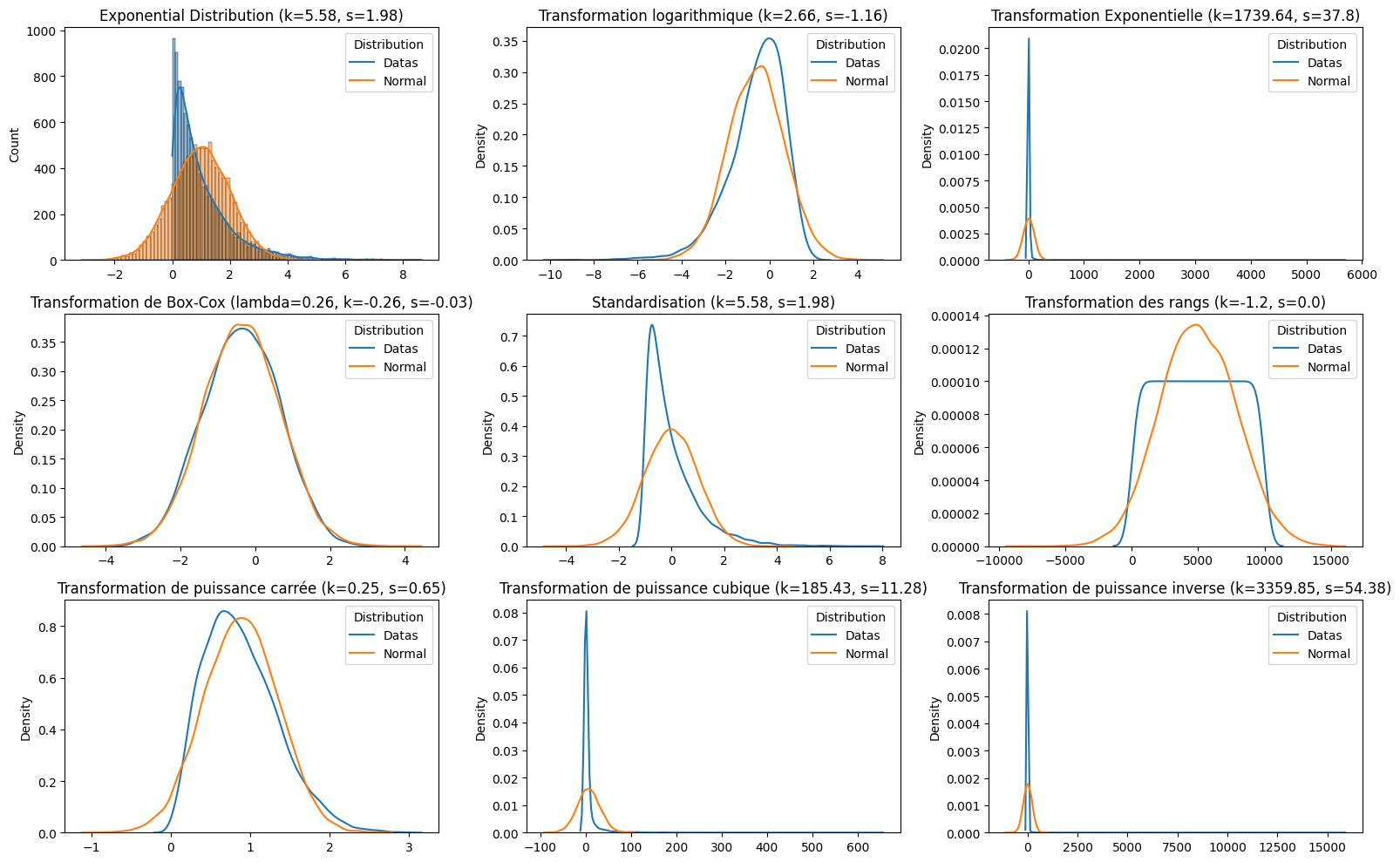
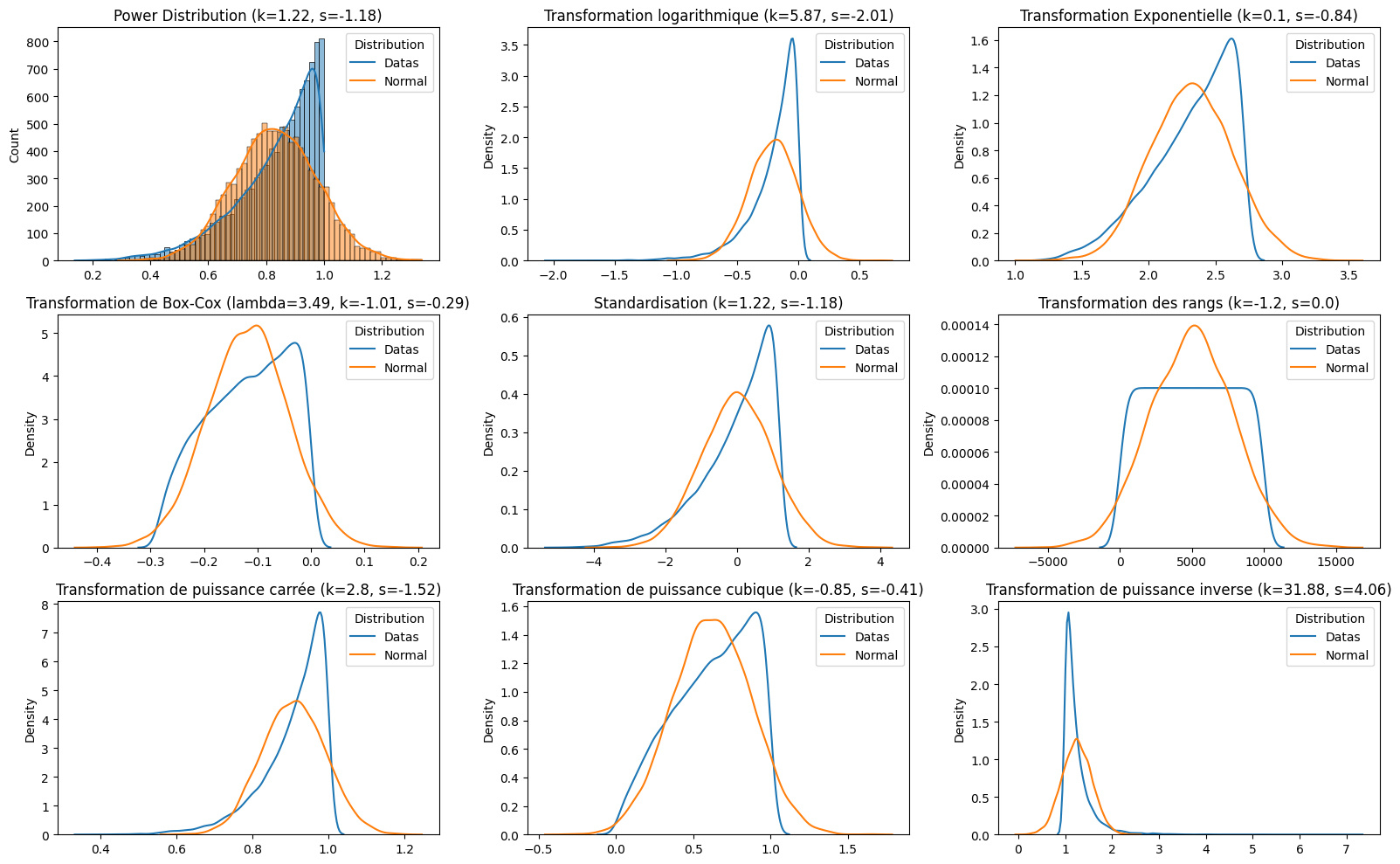
Exemple
Avec de multiples distributions possibles, on calcule la nouvelle distribution selon les différentes méthodes.
Exemple python : Fichier Python
import os
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy import stats
##################################################
def set_failed(ax, title):
ax.set_title(title)
ax.text(0.5, 0.5, "Failed", fontsize=40, ha='center', va='center', bbox=dict(facecolor='red', edgecolor='none', pad=10), color='white')
def cub(data): return data ** 3
def inv(data): return 1 / data
def standard(data): return (data - np.mean(data)) / np.std(data)
##################################################
path = os.path.join(os.path.dirname(__file__), "Figures")
os.makedirs(path, exist_ok=True) # Créer le dossier de samples (la première fois, il n'existe pas)
np.random.seed(0)
N = 10000
# Partie des fonctions de distribution possible avec Numpy
functions = [
("Beta Distribution", np.random.beta(1, 1, N)),
("Chi-square Distribution", np.random.chisquare(2, N)),
("Exponential Distribution", np.random.exponential(1, N)),
("F Distribution", np.random.f(1, 48, N)),
("Gamma Distribution", np.random.gamma(2, 2, N)),
("Gumbel Distribution", np.random.gumbel(0, 0.1, N)),
("Laplace Distribution", np.random.laplace(0, 1, N)),
("Logistic Distribution", np.random.logistic(10, 1, N)),
("Log-normal Distribution", np.random.lognormal(3, 1, N)),
("Negative binomial Distribution", np.random.negative_binomial(1, 0.1, N)),
("Noncentral chi-square Distribution", np.random.noncentral_chisquare(3, 20, N)),
("Noncentral F Distribution", np.random.noncentral_f(3, 20, 3, N)),
("Normal (Gaussian) Distribution", np.random.normal(0, 1, N)),
("Power Distribution", np.random.power(5, N)),
("Rayleigh Distribution", np.random.rayleigh(3, N)),
("Triangular Distribution", np.random.triangular(-3, 0, 8, N)),
("Von Mises Distribution", np.random.vonmises(0, 4, N)),
("Wald, or inverse Gaussian, Distribution", np.random.wald(3, 2, N)),
("Weibull Distribution", np.random.weibull(5, N))
]
transformations = [
("Transformation logarithmique", np.log), ("Transformation Exponentielle", np.exp),
("Transformation de Box-Cox", stats.boxcox), ("Standardisation", standard),
("Transformation des rangs", stats.rankdata), ("Transformation de puissance carrée", np.sqrt),
("Transformation de puissance cubique", cub), ("Transformation de puissance inverse", inv)
]
##################################################
for f in functions:
print(f[0])
# Génération de données
data = f[1]
# Création de sous-plots
fig, axes = plt.subplots(3, 3, figsize=(16, 10))
axes = axes.ravel()
# Distribution d'origine
sns.histplot(data, kde=True, ax=axes[0])
k, s = np.round(stats.kurtosis(data), 2), np.round(stats.skew(data), 2)
axes[0].set_title(f"{f[0]} (k={k}, s={s})")
normal_data = np.random.normal(np.mean(data), np.std(data), N)
sns.histplot(normal_data, kde=True, ax=axes[0])
axes[0].legend(["Datas", "Normal"], title="Distribution")
plt.show()
i = 1
for t in transformations:
try:
if t[0] == "Transformation de Box-Cox":
transformed, lambda_ = t[1](data)
l, k, s = np.round(lambda_, 2), np.round(stats.kurtosis(transformed), 2), np.round(stats.skew(transformed), 2)
if np.isnan(l) or np.isnan(k) or np.isnan(s):
set_failed(axes[i], t[0])
i += 1
continue
axes[i].set_title(f"Transformation de Box-Cox (lambda={l}, k={k}, s={s})")
else:
transformed = t[1](data)
k, s = np.round(stats.kurtosis(transformed), 2), np.round(stats.skew(transformed), 2)
if np.isnan(k) or np.isnan(s):
set_failed(axes[i], t[0])
i += 1
continue
axes[i].set_title(f"{t[0]} (k={k}, s={s})")
sns.kdeplot(transformed, ax=axes[i])
except ValueError as e:
set_failed(axes[i], t[0])
i += 1
continue
normal_data = np.random.normal(np.mean(transformed), np.std(transformed), N)
sns.kdeplot(normal_data, ax=axes[i])
axes[i].legend(["Datas", "Normal"], title="Distribution")
i += 1
# Ajustement des espacements entre les sous-graphiques
plt.tight_layout()
plt.savefig(os.path.join(path, f"{f[0]}.png"), bbox_inches="tight")