Traduction : Notes sur la BRDF de Ward

Introduction
- Notation
BRDF de Ward
- Échantillonnage
Calcul des probabilités d’échantillonnage
Limiter la BRDF
- Limitation Cosinus
- Limitation Isotrope
Conclusions
Références

Ce post est une traduction du rapport technique Notes on the Ward BRDF de Bruce Walter d’Avril 2005 disponible sur le site de l’université de Cornell ou sur Semantic Scholar

Résumé
La BRDF anisotrope introduite dans [Ward 1992] est devenue largement utilisée dans l’infographie, mais certains détails de mise en œuvre importants sont moins connus. Nous discutons de la façon d’évaluer efficacement le Ward BRDF. Ensuite, nous dérivons la fonction de densité de probabilité pour son système d’échantillonnage de Monte Carlo associé et les poids corrects à utiliser avec les échantillons générés. Enfin, pour la version isotrope, nous décrivons comment limiter la valeur BRDF maximale possible sur une région de l’espace (une direction).

Introduction

La BRDF de Ward (Bidirectional Reflectance Distribution Function ou fonction de distribution de la réflectance bidirectionnelle en français) a été introduit dans [Ward 1992] en tant que modèle empirique pour s’adapter aux données BRDF mesurées (c’est-à-dire à la réflectance de surface). Il présente plusieurs avantages par rapport aux modèles BRDF antérieurs et s’est largement répandu dans la communauté de l’infographie. Il utilise seulement quelques paramètres simples, ce qui le rend facile à contrôler, peut être échantillonné efficacement pour Monte Carlo, peut modéliser des surfaces anisotropes, et s’est avéré correspondre raisonnablement bien aux données BRDF mesurées.

Le but de cet article est de clarifier et de corriger certains détails importants de la mise en œuvre du Ward BRDF. Nous discutons de la manière d’évaluer efficacement la BRDF dans la section 2. L’échantillonnage de Monte Carlo pour la BRDF est requis pour de nombreux algorithmes de rendu, et par conséquent, Ward a fourni un schéma d’échantillonnage efficace avec sa BRDF. Cependant, il n’a pas fourni la fonction de densité de probabilité associée, qui, pour la précision mathématique, est nécessaire pour pondérer correctement les échantillons générés. Nous discutons à la fois de la façon de dériver de telles fonctions de densité de probabilité en général dans la section 3, et présentons les résultats spécifiques pour la BRDF Ward dans l’équation $\ref{eq:10}$.

Une autre puissante, mais moins largement utilisé, opération sur la BRDF est la possibilité de limiter sa valeur maximale sur une plage de directions. Dans la section 4, nous discutons de la façon de réduire le coût et de fermement limiter la BRDF de Ward isotrope sur un ensemble de directions définies par un volume de délimitation spatial.

Notation

Nous allons beaucoup travailler avec des directions en 3D, que nous désignerons en gras (par exemple, $\mathbf{v}$). En utilisation réelle, ces directions sont typiquement représentées comme des vecteurs 3D normalisés (par exemple, $\mathbf{v} = \left[v_x, v_y, v_z\right]$, où $v^2_x + v^2_y + v^2_z = 1$). Les directions peuvent également être représentées comme deux angles, $\theta$ et $\phi$, en utilisant des coordonnées polaires sphériques comme illustré sur la Figure 1. Nous incluons généralement ces angles avec la direction qu’ils décrivent. Nous pouvons convertir les coordonnées polaires sphériques et les représentations vectorielles unitaires 3D en utilisant :

\[\left( \theta ,\phi \right) \Leftrightarrow \left[ \sin \theta \cos \phi, \sin \theta \sin \phi,\cos \theta \right] \label{eq:1}\tag{1}\]

**Figure 1** : Exemple de coordonnées polaires sphériques. La direction v peut être entièrement décrite par deux angles $\theta_\mathbf{v}$ et $\phi_\mathbf{v}$ . $\theta_\mathbf{v}$ est l'angle entre v et l'axe z. $\phi_\mathbf{v}$ est l'angle entre l'axe x et la projection de v sur le plan x-y.

Le produit scalaire de deux directions est égal au cosinus de l’angle qui les sépare (par exemple, $\mathbf{v} \cdot \mathbf{z} = \cos \theta_\mathbf{v}$). Lors de l’utilisation de vecteurs 3D, le produit scalaire peut être calculé en additionnant les produits des composants correspondants (par exemple, $\mathbf{u} \cdot \mathbf{v} = u_x v_x + u_y v_y + u_z v_z$)

Une BRDF décrit comment la lumière est diffusée sur une surface. Sur un point de la surface, il s’agit d’une fonction de deux directions (une direction incidente $\mathbf{i}$ et une direction sortante $\mathbf{o}$) et écrite comme $f_r\left(\mathbf{i}, \mathbf{o}\right)$. Il est souvent pratique de construire un repère sur la surface où l’axe $\mathbf{z}$ est le même que la normale $\mathbf{n}$ locale de la surface et les axes $\mathbf{x}$ et $\mathbf{y}$ se situent dans le plan tangent de la surface, comme le montre la Figure 2. Pour les BRDF anisotropes, les axes $\mathbf{x}$ et $\mathbf{y}$ doivent correspondre aux directions principales de l’anisotropie, alors qu’ils peuvent être choisis arbitrairement pour les BRDF isotropes.

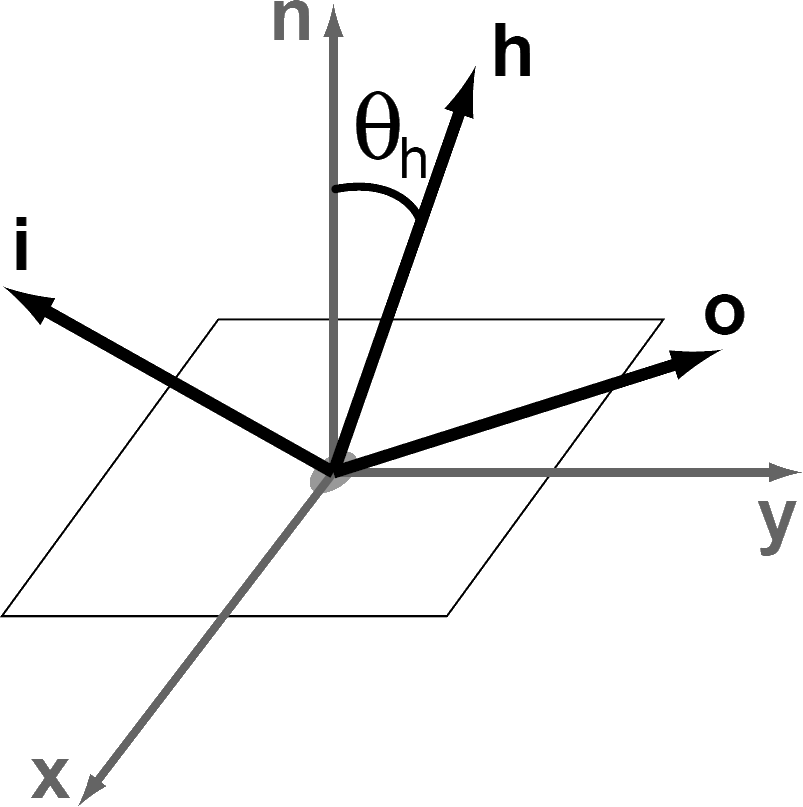
La BRDF de Ward utilise la demi-direction $\mathbf{h}$ définie à mi-chemin entre les directions incidentes et de sortie. Il peut être calculé en ajoutant $\mathbf{i}$ et $\mathbf{o}$ en tant que vecteurs 3D, puis en renormalisant:

\[\mathbf{h}=\frac{\mathbf{i} + \mathbf{o}}{\left\lVert \mathbf{i} + \mathbf{o} \right\rVert} \label{eq:2}\tag{2}\]

Le demi-angle est motivé par les microfacettes de la BRDF et produit des reflets plus réalistes que des alternatives telles que Phong (voir, par exemple, [Fisher 1994, Ngan et al., 2004]).

**Figure 2** : Repère utilisé dans les calculs de la BRDF. L'axe z est égal à la normale $\mathbf{n}$ de la surface locale, et les axes x et y se situent dans le plan tangent de la surface. La BRDF est une fonction de deux directions, la direction incidente $\mathbf{i}$ et la direction de sortie $\mathbf{o}$ (par exemple, les directions vers l'œil et la lumière). La demi-direction $\mathbf{h}$ est définie à mi-chemin entre $\mathbf{i}$ et $\mathbf{o}$ , et joue un rôle important dans la BRDF de Ward.

BRDF de Ward

La BRDF de Ward originale est défini comme la somme de deux composantes [Ward 1992, Equation 5a]. Le premier est un terme diffus, $\rho_d / \pi$. Les composants diffus sont relativement simples et déjà bien compris, donc nous ignorerons le composant diffus pour le reste de cet article. Le second composant est un lobe de brillance anisotrope gaussien défini par trois paramètres, $\rho_s$, $\alpha_x$ et $\alpha_y$, comme suit :

\[f_r(\mathbf{i}, \mathbf{o}) = \frac{\rho_s}{4 \pi \alpha_x \alpha_y \sqrt{\cos\theta_\mathbf{i} \times \cos\theta_\mathbf{o}}} \times e^{-\tan^2{\theta_\mathbf{h}} \left( \frac{\cos^2\phi_\mathbf{h}}{\alpha_x^2} + \frac{\sin^2\phi_\mathbf{h}}{\alpha_y^2} \right)} \label{eq:3}\tag{3}\]

où $\rho_s$ contrôle la grandeur du lobe, et $\alpha_x$ et $\alpha_y$ contrôlent la largeur du lobe dans les deux principales directions d’anisotropie. Si $\alpha_x = \alpha_y$ alors le lobe est isotrope (c’est-à-dire invariant sous les rotations autour de la normale de la surface). Juste après avoir défini sa BRDF, Ward présente une approximation qui est censée être moins coûteuse [Ward 1992, Equation 5b]. Il n’y a aucune raison de jamais utiliser cette approximation. L’équation vectorielle suivante est à la fois exacte et moins chère à calculer que l’approximation¹.

\[f_r(\mathbf{i}, \mathbf{o}) = \frac{\rho_s}{4 \pi \alpha_x \alpha_y \sqrt{(\mathbf{i} \cdot \mathbf{n}) \times (\mathbf{o} \cdot \mathbf{n})}} \times e^{-\frac{\left(\frac{\mathbf{h} \cdot \mathbf{x}}{\alpha_x}\right)^2 + \left(\frac{\mathbf{h} \cdot \mathbf{y}}{\alpha_y}\right)^2}{\left(\mathbf{h} \cdot \mathbf{n}\right)^2}} \label{eq:4}\tag{4}\]

Puisque $\mathbf{h}$ apparaît a des puissances égales dans le numérateur et le dénominateur de l’exposant, un demi-vecteur non normalisé peut être utilisé lors de l’évaluation de cette équation. Il est trivial de montrer que les équations $\ref{eq:3}$ et $\ref{eq:4}$ sont équivalentes en exprimant h comme un vecteur d’unité 3D comme indiqué ci-dessous et en développant les produits scalaires.

\[\mathbf{h} = \left[ \sin \theta_\mathbf{h} \cos \phi_\mathbf{h}, \sin \theta_\mathbf{h} \sin \phi_\mathbf{h},\cos \theta_\mathbf{h} \right] \label{eq:5}\tag{5}\]

Échantillonnage

Une bonne technique d’échantillonnage BRDF est essentielle dans l’efficacité des algorithmes de rendu Monte Carlo. Lors de l’échantillonnage, nous considérons que le vecteur incident i est donné, ou fixe, et que nous voulons générer des vecteurs o dans une distribution proche de la BRDF. Ward a fourni un échantillonnage pour sa BRDF [Ward 1992, Equation 7], mais a accidentellement omis un arctangent dans ses équations². Étant donné deux variables aléatoires uniformes u et v dans l’intervalle $0 < u, v < 1$, les équations d’échantillonnage correctes sont :

\[\theta_\mathbf{h} = \arctan\left(\sqrt{\frac{-log(u)}{\frac{\cos^2(\phi_\mathbf{h})}{\alpha_x^2}+\frac{\sin^2(\phi_\mathbf{h})}{\alpha_y^2}}}\right) \label{eq:6}\tag{6}\]

\[\phi_\mathbf{h} = \arctan\left(\frac{\alpha_y}{\alpha_x} \times \tan\left(2 \pi \times v \right)\right) \label{eq:7}\tag{7}\]

Il faut prendre soin de calculer le second arctangent pour garder $\phi_\mathbf{h}$ dans le même quadrant que l’angle $2\pi v$. Ces équations d’échantillonnage calculent la demi-direction $\mathbf{h}$ à partir de u et v, qui est ensuite utilisée pour générer la direction $\mathbf{o}$ à partir de $\mathbf{h}$ et $\mathbf{i}$ en utilisant :

\[\mathbf{o} = 2 \left(\mathbf{i}\cdot\mathbf{h}\right) \mathbf{h}-\mathbf{i} \label{eq:8}\tag{8}\]

Si la distribution générée des directions de sortie $\mathbf{o}$ correspond parfaitement à la BRDF, alors tous les échantillons peuvent avoir le même poids. Cependant, c’est rarement le cas pour les BRDF non triviales. Afin de calculer les poids d’échantillonnage corrects, nous devons connaître la fonction de densité de probabilité réelle po pour les directions générées o. La fonction de probabilité correcte de l’échantillonnage de Ward est:

\[p_r(\mathbf{o}) = \frac{\rho_s}{4 \pi \alpha_x \alpha_y \left(\mathbf{h} \cdot \mathbf{i}\right) \cos^3\theta_\mathbf{h}} \times e^{-\tan^2{\theta_\mathbf{h}} \left( \frac{\cos^2\phi_\mathbf{h}}{\alpha_x^2} + \frac{\sin^2\phi_\mathbf{h}}{\alpha_y^2} \right)} \label{eq:9}\tag{9}\]

Cette probabilité est, par conception, assez proche de la BRDF de Ward (voir équation $\ref{eq:3}$), mais ne correspond pas exactement. La section suivante décrira comment trouver les fonctions de probabilité d’échantillonnage et comment dériver l’équation $\ref{eq:9}$. La fonction de pondération correcte $w(\mathbf{o})$ qui doit être appliquée aux échantillons dans les algorithmes de Monte Carlo (par exemple, path tracing) est donnée par:

\[w(\mathbf{o}) = \frac{f_r(\mathbf{i}, \mathbf{o}) \times \cos\theta_\mathbf{o}}{p_o(\mathbf{o})} = \rho_s \left(\mathbf{h}\cdot\mathbf{i}\right) \left(\mathbf{h}\cdot\mathbf{n}\right)^3 \sqrt{\frac{\left(\mathbf{o}\cdot\mathbf{n}\right)}{\left(\mathbf{i}\cdot\mathbf{n}\right)}} \label{eq:10}\tag{10}\]

Les travaux antérieurs ont généralement supposé que les échantillons de la BRDF de Ward pouvaient être pondérés de façon égale (c’est-à-dire $w(\mathbf{o})\approx \rho_s$). Ceci est souvent presque vrai, mais peut causer des erreurs significatives pour les lobes larges et pour les angles rasant ou presque comme le montre la Figure 3. Pour obtenir les bons résultats dans ces cas, il faut utiliser les poids d’échantillonnage corrects de l’équation $\ref{eq:10}$.

**Figure 3** : Voici une boîte diffuse contenant une sphère avec une BRDF de Ward ( $\rho_s=0.75, \alpha_x=\alpha_y=0.15$ ). L'image de gauche est une solution de référence qui utilise un échantillonnage uniforme de l'hémisphère. L'image du milieu a utilisé l'échantillonnage de Ward mais a supposé des poids uniformes ( $w(\mathbf{o})=\rho_s$ ), tandis que l'image de droite utilisait les poids d'échantillon corrects (équation $\ref{eq:10}$ ). La rangée du bas montre les différences entre les images avec l'échantillonnage de Ward et la référence.

Certains spectateurs peuvent préférer esthétiquement l’image du milieu de la Figure 3, mais ce sont les images de gauche et de droite qui sont mathématiquement correctes pour la BRDF de Ward. L’effet d’assombrissement à proximité des angles rasant est intégré à la définition de la BRDF de Ward. [Duer 2005] a proposé de modifier ses équations pour réduire cet effet, mais cela dépasse le cadre de cet article.

Calcul des probabilités d’échantillonnage

Dans cette section, nous verrons comment calculer la densité de probabilité pour une transformation d’échantillonnage donnée et montrer comment utiliser cette théorie pour trouver la fonction de probabilité du cas isotrope de la BRDF de Ward. Nous nous intéressons spécifiquement aux densités de probabilité 2D ici, mais des relations similaires valent pour d’autres dimensions.

Théorie générale

Soit $S$ notre espace source 2D et $\left[s_1, s_2\right] \in S$ une variable aléatoire de densité de probabilité connue $p_s$. Étant donné un espace cible $T$, toute transformation de $S$ vers $T$ définit une nouvelle variable aléatoire $\left[t_1, t_2\right] \in T$ (où $t_1 = t_1 \left(s_1, s_2\right)$ et $t_2 = t_2 \left(s_1, s_2\right)$). Nous voulons calculer la densité de probabilité pt associée à la variable aléatoire transformée, $\left[t_1, t_2\right]$.

Pour simplifier, nous supposerons que la transformée est inversible sur les régions d’intérêt (c’est-à-dire que nous pouvons aussi écrire $s_1 = s_1 \left(t_1, t_2\right)$ et $s_2 = s_2 \left(t_1, t_2\right)$). La probabilité que la variable aléatoire soit dans une région $B$ (que nous écrivons comme $P(B)$) est donnée en intégrant sa densité de probabilité sur cette région par rapport à sa mesure associée (par exemple, $p_t$ et sa mesure $dt_1 dt_2$).

\[P \left( B \right) = \int_B{p_t\left(t_1, t_2 \right)\, \mathrm{d} t_1\,\mathrm{d} t_2} \label{eq:11}\tag{11}\]

Une densité de probabilité doit toujours avoir une mesure associée, bien que la mesure associée soit souvent implicite. Étant donné une région $B\subseteq T$, soit $A_B \subseteq S$ l’ensemble de tous les points de $S$ qui correspondent aux points de $B$. Les probabilités de ces deux ensembles doivent être égales (c’est-à-dire $P(A_B) = P(B)$) puisqu’elles couvrent les mêmes événements, et ainsi nous avons:

\[\int_{A_B}{p_s\left(s_1, s_2 \right)\, \mathrm{d} s_1\,\mathrm{d} s_2} = \int_B{p_t\left(t_1, t_2 \right)\, \mathrm{d} t_1\,\mathrm{d} t_2} \label{eq:12}\tag{12}\]

En appliquant le théorème du changement de variables du calcul à la première intégrale, on obtient :

\[\int_{A_B}{p_s\left(s_1, s_2 \right)\, \mathrm{d} s_1\,\mathrm{d} s_2} = \int_B{p_s\left(s_1\left(t_1, t_2\right), s_2\left(t_1, t_2\right) \right) \left\lVert \frac{\delta \left[ s_1, s_2 \right]}{\delta \left[ t_1, t_2 \right]} \right\rVert \, \mathrm{d} t_1\,\mathrm{d} t_2} \label{eq:13}\tag{13}\]

où la valeur absolue du déterminant du jacobien est définie en termes de dérivées partielles comme :

\[\left\lVert \frac{\delta \left[ s_1, s_2 \right]}{\delta \left[ t_1, t_2 \right]} \right\rVert = \begin{Vmatrix} \frac{\delta s_1}{\delta t_1} & \frac{\delta s_1}{\delta t_2} \\ \frac{\delta s_2}{\delta t_1} & \frac{\delta s_2}{\delta t_2} \\ \end{Vmatrix} = \left\lvert{\frac{\delta s_1}{\delta t_1} \frac{\delta s_2}{\delta t_2} - \frac{\delta s_2}{\delta t_1} \frac{\delta s_1}{\delta t_2}} \right\rvert \label{eq:14}\tag{14}\]

Puisque ces équations sont valables pour tout ensemble $B$, nous pouvons les utiliser pour résoudre la densité de probabilité $p_t$ comme :

\[p_t\left(t_1, t_2\right) = p_s\left(s_1\left(t_1, t_2\right), s_2\left(t_1, t_2\right) \right) \left\lVert \frac{\delta \left[ s_1, s_2 \right]}{\delta \left[ t_1, t_2 \right]} \right\rVert \label{eq:15}\tag{15}\]

Application à $p_\mathbf{h}$ et $p_\mathbf{o}$

Nous voulons spécialiser cette théorie générale pour traiter le cas spécifique de trouver des fonctions de densité de probabilité pour des méthodes d’échantillonnage basées sur la demi-direction $\mathbf{h}$ (comme la BRDF de Ward). Ces méthodes d’échantillonnage prennent deux nombres aléatoires uniformes $u$ et $v$, les transforment en une demi-direction $\mathbf{h}$, puis utilisent $\mathbf{h}$ pour générer le vecteur $\mathbf{o}$. Nous allons d’abord discuter de la dérivation de la densité de probabilité $p_h$ pour $\mathbf{h}$, puis relier cela à la densité de probabilité $p_o$ pour le vecteur de sortie $\mathbf{o}$.

Pour commencer, nous voulons appliquer l’équation $\ref{eq:15}$ où nous substituons $u, v$ pour $s_1, s_2$ et $\theta_h, \phi_h$ pour $t_1, t_2$, mais il y a une petite difficulté. Nous nous transformons en un espace non-euclidien, la sphère des directions, et la mesure appropriée à utiliser avec $p_h$ est un angle solide (c’est-à-dire que la mesure de l’angle solide est $\sin\theta_h d\theta_h d\phi_h$ plutôt que juste $d\theta_h d\phi_h$). Nous ajustons cela en incluant un facteur supplémentaire de $1 / \sin\theta_h$ pour annuler le facteur supplémentaire dans la mesure de l’angle solide pour obtenir :

\[\begin{split} p_h\left(\mathbf{h}\right) & = p_{uv}\left( u\left( \theta_h,\phi_h \right), v\left( \theta_h,\phi_h \right) \right) \left\lVert \frac{\delta \left[ u, v \right]}{\delta \left[ \theta_h,\phi_h \right]} \right\rVert \frac{1}{\sin{\theta_h}} \\ & = \left\lvert{\frac{\delta u}{\delta \theta_h} \frac{\delta v}{\delta \phi_h} - \frac{\delta v}{\delta \theta_h} \frac{\delta u}{\delta \phi_h}} \right\rvert \frac{1}{\sin{\theta_h}} \end{split} \label{eq:16}\tag{16}\]

où nous avons utilisé le fait que $p_{uv}\left(u, v\right) = 1$ puisque $u$ et $v$ sont uniformément répartis dans le carré unité.

Nous devrons également calculer $p_o$ en termes de $p_h$. La relation entre $\mathbf{h}$ et $\mathbf{o}$ peut être exprimée très simplement en utilisant le repère spécial représenté sur la Figure 4, où la direction d’incidence $\mathbf{i}$ est utilisée en tant qu’axe z. Pour les distinguer clairement, nous allons marquer tous les angles sphériques en utilisant ces coordonnées spéciales avec une étoile en exposant. La relation entre $\mathbf{h}$ et $\mathbf{o}$ dans ces coordonnées est simple : $\theta_o^*=2\theta_h^*$ et $\phi_o^*=\phi_h^*$. Nous pouvons à nouveau appliquer l’équation $\ref{eq:15}$, avec de légères modifications pour utiliser des mesures d’angle solide, pour obtenir:

\[\begin{split} p_o\left(\mathbf{o}\right) & = p_h\left(\mathbf{h}\right) \left\lVert \frac{\delta \left[ \theta_h^*,\phi_h^* \right]}{\delta \left[ \theta_o^*,\phi_o^* \right]} \right\rVert \frac{\sin{\theta_h^*}}{\sin{\theta_o^*}} \\ & = p_h\left(\mathbf{h}\right) \left\lvert{\frac{1}{2} - 0 }\right\rvert \frac{\sin{\theta_h^*}}{\sin{2\theta_o^*}}\\ & = \frac{p_h\left(\mathbf{h}\right)}{4\cos{\theta_h^*}} = \frac{p_h\left(\mathbf{h}\right)}{4\left( \mathbf{h} \cdot \mathbf{i} \right)} \end{split} \label{eq:17}\tag{17}\]

Des résultats similaires pour la demi-direction vers la direction de sortie transformée peuvent être trouvés dans [Torrance et Sparrow 1967] et [Ashikhmin et Shirley 2000].

**Figure 4** : Système de coordonnées où le vecteur incident $\mathbf{i}$ est l'axe z, et la normale de surface $\mathbf{n}$ se trouve dans le plan x-z (c'est-à-dire $\mathbf{n} \cdot \mathbf{y} = 0$ ). Comme sur la [Figure 1](#Fig1), nous pouvons spécifier des directions en utilisant deux angles sphériques, $\theta^*$ et $\theta^*$ . L'étoile indique qu'ils sont relatifs à ce repère. La relation entre $\mathbf{h}$ et $\mathbf{o}$ est, $\theta_\mathbf{o}^* = 2\theta_\mathbf{h}^*$ et $\phi_\mathbf{o}^* = \phi_\mathbf{h}^*$ .

Exemple isotrope

Maintenant, pour montrer comment appliquer ces équations pour un cas spécifique, nous allons déduire la densité de probabilité d’échantillonnage pour le cas isotrope plus simple. La BRDF de Ward est isotrope quand $\alpha_x = \alpha_y$, que l’on peut alors simplement écrire comme $\alpha$. Dans ce cas, la BRDF est simplifié à :

\[f^{iso}_r(\mathbf{i}, \mathbf{o}) = \frac{\rho_s}{4 \pi \alpha^2 \sqrt{\cos\theta_\mathbf{i} \times \cos\theta_\mathbf{o}}} \times e^{-\frac{\tan^2{\theta_\mathbf{h}}}{\alpha^2}} \label{eq:18}\tag{18}\]

et les équations d’échantillonnage isotropes sont simplifiés à :

\[\theta_\mathbf{h} = \arctan\left(\alpha\sqrt{-log(u)}\right) \label{eq:19}\tag{19}\]

\[\phi_\mathbf{h} = 2 \pi \times v \label{eq:20}\tag{20}\]

Nous pouvons inverser ces équations d’échantillonnage isotropes pour obtenir :

\[u = e^{-\frac{\tan^2{\theta_\mathbf{h}}}{\alpha^2}} \label{eq:21}\tag{21}\]

\[v = \frac{\phi_\mathbf{h}}{2 \pi} \label{eq:22}\tag{22}\]

Ensuite, nous pouvons appliquer l’équation $\ref{eq:16}$ et calculer les dérivées partielles de $u$ et $v$ par rapport à $\theta_h$ et $\phi_h$ pour obtenir :

\[\begin{split} p^{iso}_h\left(\mathbf{h}\right) & = \left\lvert{ \left( e^{-\frac{\tan^2{\theta_\mathbf{h}}}{\alpha^2}} \frac{2\tan{\theta_h}}{\alpha^2\cos^2_{\theta_h}} \right) \left( -\frac{1}{2\pi} \right) - \left( 0 \right)\left( 0 \right) }\right\rvert \frac{1}{\sin{\theta_h}} \\ & = \frac{1}{\pi\alpha^2\cos^3_{\theta_h}} \times e^{-\frac{\tan^2{\theta_\mathbf{h}}}{\alpha^2}} \end{split}\label{eq:23}\tag{23}\]

où nous avons supprimé l’opération de valeur absolue car elle est toujours positive dans l’interval valide de $\theta_h$, entre zéro et $\pi / 2$. Enfin, nous utilisons l’équation $\ref{eq:17}$, nous obtenons la densité de probabilité pour la direction $\mathbf{o}$ échantillonnée dans le cas isotrope comme :

\[p^{iso}_h\left(\mathbf{o}\right) = \frac{1}{4\pi\alpha^2\left(\mathbf{h}\cdot\mathbf{i}\right)\cos^3_{\theta_h}} \times e^{-\frac{\tan^2{\theta_\mathbf{h}}}{\alpha^2}} \label{eq:24}\tag{24}\]

La dérivation de l’équation $\ref{eq:9}$ pour le cas anisotrope est effectuée de manière similaire avec vérification laissée comme un exercice pour le lecteur.

Limiter la BRDF

Une autre opération utile de la BRDF consiste à limiter sa valeur maximale dans un ensemble de directions. Bien qu’il s’agisse d’une opération beaucoup moins courante que l’échantillonnage, il s’agit d’une opération puissante requise par certains algorithmes de rendu [Walter et al. 2005]. Dans cette section, nous allons décrire comment calculer une limite raisonnablement peu couteuse et proche de la BRDF de Ward isotrope. L’extension à la version anisotrope plus générale reste à venir.

Lors de la délimitation de la BRDF, la direction d’incidence $\mathbf{i}$ et le point de surface sont considérés comme fixes, mais la direction de sortie $\mathbf{o}$ peut varier. Nous pouvons spécifier l’ensemble des directions autorisées à l’aide d’un volume englobant $\mathcal{B}$ comme indiqué dans la Figure 5. Pour simplifier, supposons que le point de réflexion de la surface soit à l’origine. Soit $\vec{v}$ un vecteur 3D; la flèche indique que c’est un vecteur de longueur arbitraire plutôt qu’une direction normalisée. Nous voulons calculer une borne supérieure sur une fonction de $\mathbf{o}$, (c’est-à-dire la BRDF dans notre cas), sur tout $\mathbf{o} = \vec{v} / \lVert \vec{v} \rVert$ où $\vec{v} \in \mathcal{B}$.

Une solution standard consisterait à utiliser l’arithmétique d’intervalles. En remplaçant chaque opérateur par son équivalent d’intervalle et en exprimant le volume englobant comme des intervalles, le calcul d’une limite supérieure serait simple. Malheureusement, ces limites d’intervalle tendent à être plutôt lâches, surtout si les intervalles initiaux sont grands. Au lieu de cela, nous allons essayer de trouver une direction ou un ensemble de paramètres qui est une limite supérieure stricte et correspond à un point dans ou à proximité du volume englobant.

**Figure 5** : Limitation de la valeur maximale de la BRDF. Les directions incidentes et normales sont fixes et le point de réflexion est supposé être à l'origine. Nous calculons ensuite une borne supérieure sur $f_r\left(\mathbf{i},\mathbf{o}\right)$ sur un ensemble de directions de sortie définies par un volume de limitation $\mathcal{B}$ . Les directions de sortie autorisées sont $\mathbf{o}=\vec{v} / \left\lVert \vec{v} \right\rVert$ pour tout $\vec{v} \in \mathcal{B}$ .

Limitation Cosinus

Commençons par le problème relativement simple du calcul d’une borne supérieure sur $\cos\theta_o$ sur le volume englobant $\mathcal{B}$. Si nous utilisons un système de coordonnées où la normale de surface $\mathbf{n}$ est l’axe z (i.n., Figure 2) et que $\mathbf{o} = \vec{v} / \lVert \vec{v} \rVert$, alors nous pouvons écrire ceci :

\[\cos{\theta_o} = \left( \mathbf{o} \cdot \mathbf{z} \right) = \frac{1}{\sqrt{v^2_x + v^2_y + v^2_z}} \label{eq:25}\tag{25}\]

La dérivée de $\cos\theta_o$ par rapport à $v_z$ est toujours positive, donc on peut remplacer $v_z$ par sa valeur maximale sur le volume englobant $\mathcal{B}$ pour obtenir :

\[\cos{\theta_o} \leq \frac{\max{\left(v_z\right)}}{\sqrt{v^2_x + v^2_y + \left[ \max{\left(v_z\right)} \right]^2}} \label{eq:26}\tag{26}\]

Maintenant que le signe du numérateur est fixe, nous pouvons sélectionner $v_x$ et $v_y$ pour minimiser ou maximiser le dénominateur de façon appropriée :

\[\cos{\theta_o} \leq \begin{cases} \frac{\max{\left(v_z\right)}}{\sqrt{\min{\left(v^2_x\right)} + \min{\left(v^2_y\right)} + \left[ \max{\left(v_z\right)} \right]^2}} & \text{if} \max{\left(v_z\right)} \geq 0\\ \frac{\max{\left(v_z\right)}}{\sqrt{\max{\left(v^2_x\right)} + \max{\left(v^2_y\right)} + \left[ \max{\left(v_z\right)} \right]^2}} & \text{otherwise} \end{cases} \label{eq:27}\tag{27}\]

Un exemple est montré dans la Figure 6. Notez que nous choisissons la valeur maximum de $v_z$ mais pour $v_x$ et $v_y$ nous choisissons les valeurs qui maximisent ou minimisent leurs valeurs au carré. Ainsi, si $v_x$ peut varier de $-2$ à $1$, alors $\max{\left(v_x\right)} = 1$, mais $\max{\left(v^2_x\right)} = 4$ et $\min{\left(v^2_x\right)} = 0$.

**Figure 6** : Exemple de limitation de la valeur maximale de $\cos{\theta_\mathbf{o}}$ à l'aide de l'équation $\ref{eq:27}$ .

Limitation Isotrope

Pour lier la BRDF de Ward isotropique (équation $\ref{eq:18}$), nous commençons par borner son terme exponentiel en calculant une borne inférieure pour $\tan\theta_h$. Ou de manière équivalente, puisque $0\leq \theta_h \leq \pi / 2$, on peut calculer une borne supérieure sur $\cos\theta_h = \left(\mathbf{h} \cdot \mathbf{n}\right)$. Nous utiliserons le système de coordonnées de la Figure 4 en raison de sa relation simple entre $\mathbf{o}$ et $\mathbf{h}$. En exprimant $\mathbf{h}$ et $\mathbf{n}$ comme des vecteurs unitaires 3D basés sur leurs coordonnées sphériques et en notant que $\phi_n^* = 0$, nous obtenons :

\[\begin{split} \left(\mathbf{h} \cdot \mathbf{n}\right) & = \left[ \sin \theta_\mathbf{h}^* \cos \phi_\mathbf{h}^*, \sin \theta_\mathbf{h}^* \sin \phi_\mathbf{h}^*,\cos \theta_\mathbf{h}^* \right] \cdot \left[ \sin \theta_\mathbf{n}^*, 0, \cos \theta_\mathbf{n}^* \right] \\ & = \sin \theta_\mathbf{n}^*\sin \theta_\mathbf{h}^*\cos \phi_\mathbf{h}^* + \cos \theta_\mathbf{n}^*\cos \theta_\mathbf{h}^* \end{split} \label{eq:28}\tag{28}\]

Puisque $\theta_n^*$ est fixe, il suffit de sélectionner les valeurs appropriées pour $\theta_h^*$ et $\phi_h^*$ qui maximisent cette expression.

La dérivée de $\left(\mathbf{h} \cdot \mathbf{n}\right)$ par rapport à $\cos\phi_h^*$ est toujours positive, donc on peut remplacer $\cos\phi_h^*$ par sa valeur maximale sur le volume englobant $\mathcal{B}$. En utilisant le repère de la Figure 4 pour exprimer les points $\vec{v}^* \in \mathcal{B}$ et puisque $\phi_\mathbf{h}^* = \phi_\mathbf{o}^*$ nous avons :

\[\cos \phi_\mathbf{h}^* = \cos \phi_\mathbf{o}^*= \frac{v_y^*}{\sqrt{\left( v_x^* \right)^2+\left( v_y^* \right)^2}} \label{eq:29}\tag{29}\]

et nous pouvons calculer une borne sur le maximum de $\cos\phi_h^*$ de la même manière que nous l’avons fait pour l’équation $\ref{eq:27}$.

La situation pour $\theta_h^*$ est plus compliquée. Nous pouvons calculer un intervalle de limites de valeurs possibles pour $\cos\theta_h^*$ en utilisant l’équation $\ref{eq:27}$ pour limiter sa valeur maximale et une équation analogue pour limiter son minimum. Ensuite, nous pouvons utiliser la formule du demi-angle de la trigonométrie :

\[\cos \theta_\mathbf{h}^* = \cos {\frac{\theta_\mathbf{o}^*}{2}} = \sqrt{\frac{1+\cos\theta_\mathbf{o}^*}{2}} \label{eq:30}\tag{30}\]

pour transformer cela en un intervalle limité au $\cos\theta_h^*$. Pour sélectionner la valeur appropriée à partir de cet intervalle, nous devons connaître la valeur qui maximiserait $\left(\mathbf{h} \cdot \mathbf{n}\right)$. Nous pouvons résoudre la valeur de maximisation de $\cos\theta_h^*$ en prenant l’équation pour $\left(\mathbf{h} \cdot \mathbf{n}\right)$, en remplaçant $\cos\phi_h^*$ par sa borne supérieure, puis en prenant la dérivée par rapport à $\theta_h^*$ et en la définissant égale à zéro. La valeur de maximisation de $\cos\theta_h^*$ est donc donnée par :

\[\frac{\delta\left( \mathbf{h} \cdot \mathbf{n} \right)}{\delta\theta_\mathbf{h}^*} = 0\]

\[\sin \theta_\mathbf{n}^*\sin \theta_\mathbf{h}^*\max{\left(\cos \phi_\mathbf{h}^*\right)} - \cos \theta_\mathbf{n}^*\sin \theta_\mathbf{h}^* = 0\]

\[\tan\theta_h^* = \frac{\sin\theta_n^*\max{\left(\cos \phi_\mathbf{h}^*\right)}}{ \cos \theta_\mathbf{n}^*}\]

\[\cos{\theta_h^*} = \left\{ \begin{array}{cl} \sqrt{\frac{\cos^2{\theta_n^*}}{\cos^2{\theta_n^*} + \sin^2{\theta_n^*}\left[ \max{\left(\cos\phi_h^*\right)} \right]^2 }} & \text{if} \max{\left(\cos\phi_h^*\right)} \geq 0\\ 1 & \text{otherwise} \end{array} \right. \label{eq:31}\tag{31}\]

où les deux cas sont nécessaires parce que lorsque $\max\left(\cos\phi_h^*\right)$ est négatif, il en est de même pour l’angle de maximisation, mais les valeurs négatives pour $\theta_h^*$ ne sont pas autorisées et doivent être bloquées à zéro. Nous avons également utilisé l’identité $\cos\theta_h^* = \sqrt{1 / \left( 1 + \tan\theta_h^* \right)}$ pour $0 \leq \theta_h^* \leq \pi / 2$.

Notez que dans le plan d’incidence (c’est-à-dire $\max\left(\cos\phi_h^*\right) = 1$), le maximum se produit lorsque $\theta_h^*= \theta_n^*$, comme prévu. Cependant, à partir du plan d’incidence, nous devons résoudre explicitement l’angle de maximisation, car les lobes à demi-direction ne sont pas symétriques par rapport à la direction de la réflexion. Notez également que nous avons besoin que $\theta_n^*$ soit dans l’intervalle $0 \leq \theta_n^* \leq \pi / 2$.

Maintenant, nous sélectionnons la valeur de notre intervalle englobant de $\cos\theta_h^*$ qui est la plus proche de la valeur maximisante donnée par l’équation $\ref{eq:31}$, et la remplaçons avec $\max\left(\cos\phi_h^*\right)$ dans l’équation $\ref{eq:28}$ pour obtenir la limite supérieure désirée $\left(\mathbf{h} \cdot \mathbf{n}\right)$ sur le volume englobant $\mathcal{B}$.

Ce que nous voulons finalement, c’est une limitation sur :

\[f^{iso}_r\left(\mathbf{i}, \mathbf{o}\right)\cos\theta_o = \frac{\rho_s}{4 \pi \alpha^2} \times \sqrt{\frac{\cos\theta_o}{\cos\theta_i}} \times e^{-\frac{\tan^2{\theta_\mathbf{h}}}{\alpha^2}} \label{eq:32}\tag{32}\]

Nous pouvons mettre une borne supérieure sur $\cos\theta_o$ en utilisant l’équation $\ref{eq:27}$ et nous avons une borne supérieure sur $\left(\mathbf{h} \cdot \mathbf{n}\right)$ que nous pouvons convertir en borne inférieure sur $\tan^2{\theta_\mathbf{h}}$ en utilisant l’identité:

\[\tan^2{\theta_\mathbf{h}} = \frac{1-\left(\mathbf{h} \cdot \mathbf{n}\right)^2}{\left(\mathbf{h} \cdot \mathbf{n}\right)^2} \label{eq:33}\tag{33}\]

étant donné que $0 \leq \theta_h \leq \pi / 2$. En les assemblant, on obtient la limite désirée pour la BRDF de Ward isotrope.

Conclusions

Dans cet article, nous avons discuté de la BRDF de Ward et de plusieurs questions importantes pour ceux qui veulent l’utiliser. Nous avons examiné comment évaluer et échantillonner efficacement la BRDF de Ward. Nous avons ensuite dérivé la densité de probabilité associée au plan d’échantillonnage de Ward et donné les poids corrects à utiliser avec les échantillons. Pour l’exactitude mathématique, ces poids doivent être utilisés dans tout algorithme de Monte Carlo qui utilise l’échantillonnage de Ward. Nous avons également décrit comment limiter efficacement la BRDF de Ward isotrope sur un ensemble de direction pour les algorithmes de rendu qui nécessitent des limites de BRDF.

Références

ASHIKHMIN, M., AND SHIRLEY, P. S. 2000. An anisotropic phong BRDF model. Journal of Graphics Tools 5, 2, 25–32.
DUER, A. 2005. On the Ward model for global illumination. not yet published.
DUTRE, P., 2001. Global illumination compendium. Web document. http://www.cs.kuleuven.ac.be/phil/GI/TotalCompendium.pdf.
FISHER, F. 1994. R.E versus N.H specular highlights. In Graphics Gems IV. 388–400.
LARSON, G. W., AND SHAKESPEARE, R. 2004. Rendering with radiance: the art and science of lighting visualization. Booksurge Llc.
NGAN, A., DURAND, F., AND MATUSIK, W., 2004. Experimental validation of analytical BRDF models. Technical Sketch, SIGGRAPH 2004. (slides online).
TORRANCE, K. E., AND SPARROW, E. M. 1967. Theory for offspecular reflection from roughened surfaces. Journal of the Optical Society of America 57, 9, 1105–1114.
WALTER, B., FERNANDEZ, S., ARBREE, A., BALA, K., DONIKIAN, M., AND GREENBERG, D. P. 2005. Lightcuts: A scalable approach to illumination. ACM Transactions on Graphics (July). (to appear SIGGRAPH 2005).
WARD, G. J. 1992. Measuring and modeling anisotropic reflection. In Computer Graphics (Proceedings of SIGGRAPH 92), vol. 26, 265–272.
WARD, G., 2004. Behavior of materials in radiance. Web document. http://radsite.lbl.gov/radiance/refer/materials.pdf.

Cette forme vectorielle a été trouvée indépendamment par plusieurs personnes dont moi-même. Greg Ward attribue Cristophe Schlick comme étant le premier. Des formulations équivalentes peuvent également être trouvées dans [Ward 2004] et des versions récentes de [Larson et Shakespeare 2004]. ↩
L’arctangent manquant a d’abord été signalé à Alex Ward par Greg Ward et peut également être trouvé dans [Dutre 2001] ↩

Thibaut Monseigne

Ingénieur Recherche et Développement en Interface Cerveau-Machine.