Mémo Géometrie dans l'espace
Quelques Conventions / Définitions
Voici quelques définitions d’objets généraux utilisé par la suite.
| Origine : | \(\mathcal{O}\) | Centre : | \(\mathcal{C}\). | Direction : | \(\mathcal{D}\) | Rayon (cercle, sphère) : \(\mathcal{r}\) | Diamètre (cercle, sphère) : \(\mathcal{d}\) |
| Point : | \(\mathcal{P}\) | Normale : | \(\mathcal{N}\) | Vecteurs : | \(V\) ou \(\vec{v}\) | Coordonnées dans l’espace : | \((x,y,z)\) ou \((\vec{u},\vec{v},\vec{w})\) |
| Espace quelconque : | \(\mathcal{E}\) |
| Espace muni d’un repère orthonormé direct \((\mathcal{O},\vec{i},\vec{j},\vec{k})\) : | \(\mathcal{E_\bot}\) |
| Rayon : | \(\mathcal{R}\) | Origine : | \(\mathcal{R_O}\) | Direction : | \(\mathcal{R_D}\) | Equation : | \(\mathcal{R}(t) = \mathcal{R_D}\times t + \mathcal{R_O}\) |
| Sphère : | \(\mathcal{S}\) | Centre : | \(\mathcal{S_C}\) | Rayon : | \(\mathcal{S_r}\) | Equation : | \({\lVert p-\mathcal{S_C}\rVert}^2-\mathcal{S_r}^2 = 0\) |
| Plan : | \(\mathcal{P}\) | Origine : | \(\mathcal{P_O}\) | Normale : | \(\mathcal{P_N}\) | Equation : | \(\left( p-\mathcal{P_O} \right)\cdot \mathcal{P_N} = 0\) |
\(\times\) correspond à multiplier sauf lorsque l’un a deux vecteurs, il s’agit du produit croisés, on utilisera * à la place.
Mémo Trigonométrie
Mémo Espace vectoriel
Intersection
Pour calculer une intersection à partir d’équation, il suffit de trouver un point commun à ces équations.
L’ensemble des points d’un rayon \(\mathcal{R}\) obéi à la fonction affine \(\mathcal{R}(t) = \mathcal{R_D}\times t + \mathcal{R_O}\) où \(t\) pourrait être symbolisé comme le temps passé sur le rayon (demi-droite, car t ne doit pas être inférieur à 0).
Rayon (demi-droite) / Sphère
Voici l’équation de l’ensemble des points \(\mathcal{p}\) d’une sphère de centre \(\mathcal{S_C}\) et de rayon \(\mathcal{S_r}\) : \({\lVert \mathcal{p}-\mathcal{S_C}\rVert}^2-\mathcal{S_r}^2 = 0\)
On substitue \(\mathcal{p}\) par \(\mathcal{R}(t)\) :
| \({\lVert \mathcal{R}(t)-\mathcal{S_C}\rVert}^2-\mathcal{S_r}^2\) | \(=\) | \(0\) |
| \({\lVert \mathcal{R_D}\times t + \mathcal{R_O}-\mathcal{S_C}\rVert}^2-\mathcal{S_r}^2\) | \(=\) | \(0\) |
On n’oublie pas que \(t\) et \(\mathcal{S_r}\) ne sont que des nombres et le reste des vecteurs. Mais aussi qu’une norme carrée n’est rien de plus qu’un produit scalaire d’un vecteur par lui-même et la distributivité fonctionne comme pour une multiplication normale. On va prendre \(\mathcal{OC} = \mathcal{R_O}-\mathcal{S_C}\)
| \({\lVert \mathcal{R_D}\times t\rVert}^2 + 2\times t \times \mathcal{R_D} \cdot \mathcal{OC} + {\lVert\mathcal{OC}\rVert}^2-\mathcal{S_r}^2\) | \(=\) | \(0\) |
| \({\lVert \mathcal{R_D} \rVert}^2 \times t^2 + 2 \times \left( \mathcal{R_D} \cdot \mathcal{OC} \right) \times t + {\lVert\mathcal{OC}\rVert}^2-\mathcal{S_r}^2\) | \(=\) | \(0\) |
On a une équation de la forme \(ax^2+bx+c=0\) avec : \(\begin{cases} a & = & {\lVert \mathcal{R_D} \rVert}^2\\ b & = & 2 \times \left( \mathcal{R_D} \cdot \mathcal{OC} \right)\\ c & = & {\lVert\mathcal{OC}\rVert}^2-\mathcal{S_r}^2\end{cases}\)
Pour la résoudre il nous faut un delta tel que : \(\Delta = b^2-4ac\).
On a trois cas de figure :
- \(\Delta < 0\) : Il n’y a aucune solution (dans notre cas, pas d’intersection).
- \(\Delta = 0\) : Il n’y a qu’une solution : \(t = -\frac{b}{2a}\).
- \(\Delta > 0\) : Il y a deux solutions : \(t_1 = -\frac{b-\sqrt{\Delta}}{2a}\) et \(t_2 = -\frac{b+\sqrt{\Delta}}{2a}\)
Si \(t<0\) on ne le prend pas, car il se situe avant l’origine du rayon.
Rayon (demi-droite) / Plan
Voici l’équation de l’ensemble des points \(\mathcal{p}\) du plan qui possède le point \(\mathcal{P_O}\) et la normale \(\mathcal{P_N}\) : \(\left( p-\mathcal{P_O} \right)\cdot \mathcal{P_N} = 0\)
On substitue \(\mathcal{p}\) par \(\mathcal{R}(t)\) :
| \(\left(\mathcal{R}(t)-\mathcal{P_O} \right)\cdot \mathcal{P_N}\) | \(=\) | \(0\) | |||
| \(\left(\mathcal{R_D}\times t + \mathcal{R_O}-\mathcal{P_O} \right)\cdot \mathcal{P_N}\) | \(=\) | \(0\) | \(\quad\) | avec : | \(\mathcal{RP} = \mathcal{R_O}-\mathcal{P_O}\) |
| \(\left(\mathcal{R_D}\times t \right) \cdot \mathcal{P_N} + \mathcal{RP} \cdot \mathcal{P_N}\) | \(=\) | \(0\) | |||
| \(t \times \left(\mathcal{R_D} \cdot \mathcal{P_N}\right) + \left(\mathcal{RP} \cdot \mathcal{P_N}\right)\) | \(=\) | \(0\) |
On a quatre cas de figure :
- \(\mathcal{R_D} \cdot \mathcal{P_N} = 0\) : Il n’y a aucune solution les vecteurs sont orthogonaux il n’y a donc pas d’intersection.
- \(\mathcal{R_D} \cdot \mathcal{P_N} \approx 0\) : Il n’y a aucune solution, car \(t\) est proche de l’infini.
- \(t < 0\) : On ne le prend pas, car il se situe avant l’origine du rayon.
- \(t > 0\) : On a notre solution
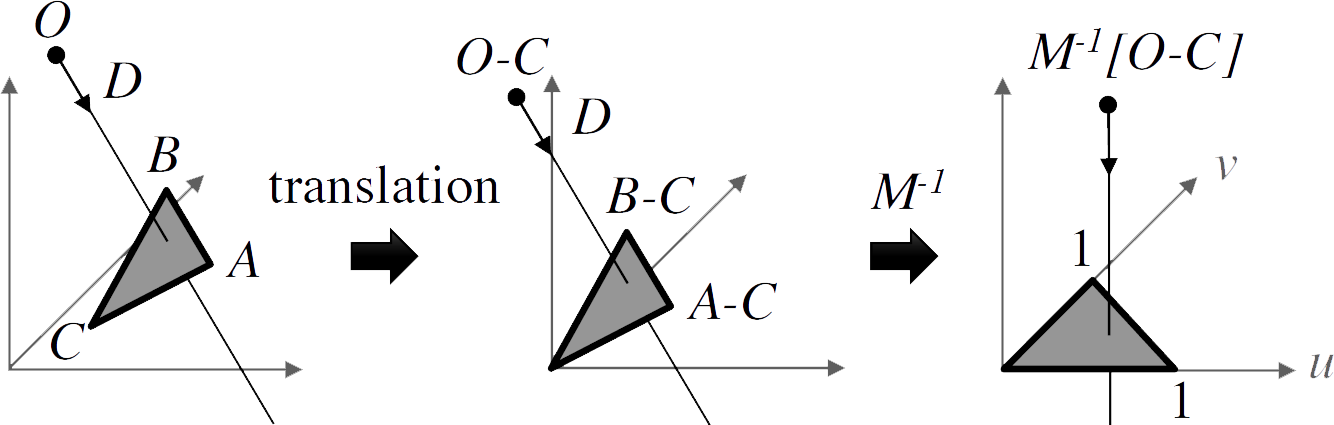
Rayon (demi-droite) / Triangle
Pour ce faire nous allons utiliser la méthode de Möller-Trumbore : On a \(A\), \(B\) et \(C\) les points du triangle, \(\mathcal{R_O}\) l’origine du rayon, \(\mathcal{R_D}\) sa direction.
On commence par translater le triangle pour le ramener à l’origine (on soustrait \(C\) à \(A\) et \(B\) mais aussi à \(\mathcal{R_O}\) pour avoir un \(t\) translaté également. Ensuite on aura besoin de différents déterminants de trois vecteurs.
Rappel Déterminant : \(\left\lvert A \quad B \quad C \right\rvert = -\left(A \times B \right) \cdot C = -\left(C \times B \right) \cdot A\)
avec \(\begin{cases} E_1 & = & A-C\\ E_2 & = & B-C\\ T & = & \mathcal{R_O}-C\end{cases}\), on a :
On a trois cas de figure :
- \(t < 0\) : On ne le prend pas, car il se situe avant l’origine du rayon.
- \(t > 0\) : On a notre solution mais
- \(u < 0\) ou \(v < 0\) ou \(u + v > 1\) : On est en dehors du triangle
- \(u > 0\) et \(v > 0\) et \(u + v < 1\) : On est dans le triangle et on a ses coordonnées de mapping.
Transformation
Pour effectuer une transformation dans l’espace, il suffit de faire le produit matriciel du Point 3D \(\mathcal{P}\) avec une matrice de transformation \(\mathcal{M}\). On va pondérer le point 3D avec une quatrième coordonnée \(w\). Cet ajout permettra d’effectuer une translation avec un produit matriciel. Pour retrouver le point 3D on divise chaque coordonnée par w (normalement au fil des transformations il doit rester à 1).
Rappel Matrice Identité et enchainement
La matrice Identité est une matrice qui multiplié à un point donne le même point.
La multiplication de différentes matrices de transformation permet d’obtenir une nouvelle matrice qui sera l’application de toute ses transformations successives. Evidemment, changer l’ordre des transformations peut changer le résultat.
Translation
Pour déplacer un point \(\mathcal{P}\) par le vecteur \(\vec{T}\), la matrice de translation sera :
Homothétie
Pour multiplier la distance à l’origine d’un point \(\mathcal{P}\) par le facteur \(H\), la matrice d’homothétie sera :
Rotation
Rotation d’un point P par l’angle θ centré sur l’origine, la matrice de rotation sera (autour d’un axe \(x\), \(y\) ou \(z\)) :
Repère global VS Repère Local
Le repère global est le repère de l’espace, il est commun à tous les objets et ne change pas. Le repère local quant à lui est le repère de l’objet en lui-même. Lorsque l’on déplace l’objet, le repère se déplace lui aussi. Ainsi, un point qui se situe aux coordonnées \((x,y,z)\) du repère local aura toujours les mêmes coordonnées dans le repère local une fois déplacé.
Enchainement de Transformation
Si on veut effectuer une rotation et une translation, on peut multiplier les deux matrices de transformations. Mais l’ordre est important si on fait une rotation puis une translation ne donne pas le même résultat qu’une translation puis une rotation.
Mais comment les enchainer et les lire ? Pour les enchaîner c’est simple, il suffit de multiplier les matrices, une multiplication de matrice carré d’ordre n donnera une matrice carré d’ordre n. Donc aucun problème. En réalité tout dépend de comment on réfléchit, Si on travaille dans le repère global, il faut lire les enchainements de transformation de droite à gauche, si on pense en repère local, il faut lire de gauche à droite.